逻辑斯蒂函数

Posted on

逻辑斯蒂函数

逻辑斯蒂函数由比利时数学家皮埃尔·弗朗索瓦·韦吕勒（Pierre François Verhulst，1804 - 1849）提出，并在后来的岁月中被他人证实，已成为生物检定中的基本工具之一，并且在统计学、经济学和流行病学等多个领域得到了越来越广泛的应用。

逻辑斯蒂函数的微分形式

\[ \begin{equation} \frac{\mathrm{d} P(t)}{\mathrm{d} t} = rP(t)\left(1-\frac{P(t)}{K}\right) \end{equation} \]

  • \(P(t)\) 是种群在时间 \(t\) 的大小
  • \(r\) 是种群的增长率
  • \(K\) 是环境的承载能力

逻辑斯蒂函数

\[ \begin{equation} P(t) = \frac{K P_0 e^{rt}}{K+P_0(e^{rt} - 1)} \end{equation} \]

其中 \(P_0\) 是初始种群大小。逻辑斯蒂函数的图像呈S形，表示种群在初期快速增长，随后逐渐减缓，最终趋于稳定。

求解过程：

\[ \begin{aligned} \frac{\mathrm{d}P}{\mathrm{d}t} &= rP\left(1-\frac{P}{K}\right)\\[10pt] \frac{\mathrm{d}P}{\mathrm{d}t} &= \frac{r}{K}P(K-P)\\[10pt] \int\frac{1}{P(K-P)}\mathrm{d}P &= \int\frac{r}{K}\mathrm{d}t \\[10pt] \frac{1}{K}\int\left(\frac{1}{P} + \frac{1}{K-P}\right)\mathrm{d}P &= \frac{r}{K}t + C_1\\[10pt] \ln |P| - \ln |K-P| &= rt + C_2\\[10pt] \frac{P}{K-P} &= Ae^{rt} \text{ , where } A=\pm e^{C_2}\text{ or }A=\frac{P_0}{K-P_0}\\[10pt] P &= (K - P)Ae^{rt}\\[10pt] (1 + Ae^{rt})P &= K Ae^{rt}\\[10pt] P &= \frac{K}{1 + A^{-1} e^{-rt}} = \frac{K}{1 + \frac{K-P_0}{P_0} e^{-rt}}\\[10pt] &= \frac{K P_0 e^{rt}}{K+P_0(e^{rt} - 1)} \end{aligned} \]


将 \((2)\) 代入 \((1)\) ，得到逻辑斯蒂微分函数

\[ \begin{equation} \frac{\mathrm{d}P(t)}{\mathrm{d}t} = \frac{rKP_0e^{rt}(K-P_0)}{(K+P_0e^{rt} - P_0)^2} \end{equation} \]

代入过程：

\[ \begin{aligned} \frac{\mathrm{d}P}{\mathrm{d}t} &= r\frac{K P_0 e^{rt}}{K+P_0(e^{rt} - 1)}\left(1-\frac{P_0 e^{rt}}{K+P_0(e^{rt} - 1)}\right)\\[20pt] &=r\frac{K P_0 e^{rt}}{K+P_0(e^{rt} - 1)}-r\frac{K P_0 e^{rt}}{K+P_0(e^{rt} - 1)}\frac{P_0 e^{rt}}{K+P_0(e^{rt} - 1)}\\[20pt] &= \frac{rKP_0e^{rt}(K+P_0e^{rt} - P_0)-rKP_0^2e^{2rt}}{(K+P_0(e^{rt} - 1))^2}\\[20pt] &= \frac{rK^2P_0e^{rt}+rKP_0^2e^{2rt}-rKP_0^2e^{rt}-rKP_0^2e^{2rt}}{(K+P_0e^{rt} - P_0)^2}\\[20pt] &= \frac{rK^2P_0e^{rt}-rKP_0^2e^{rt}}{(K+P_0e^{rt} - P_0)^2}\\[20pt] &= \frac{rKP_0e^{rt}(K-P_0)}{(K+P_0e^{rt} - P_0)^2} \end{aligned} \]


COVID-19的逻辑斯蒂模型

使用逻辑斯蒂模型来拟合COVID-19的传播数据。可以通过最小二乘法来估计模型参数 \(K\) 、 \(r\) 和 \(P_0\) 。选取2020年1月20日至2020年3月13日湖北省的每日累计确诊数据作为拟合数据区间，通过非线性拟合方法建立逻辑斯蒂函数模型，以描述病毒传播过程中的增长规律。

我在这里只对数据做了拟合计算，没有对拟合结果的好坏做分析，因为这超出了本文主题，也超出了我的知识范围（我没有相关的统计学知识）。

数据获取

原始数据可以在github上找到： 2019-nCoV 全量每日统计数据（支持接口读取）

数据处理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
import os
import pandas as pd
import numpy as np

# 数据的路径
data_path = './Wuhan-2019-nCoV-master/Data/'

# 读取csv文件
csv_files = [f for f in os.listdir(data_path) if f.endswith('.csv')]

# 将读取到的csv文件合并为一个DataFrame
df_list = [pd.read_csv(os.path.join(data_path, f), encoding='utf-8') for f in csv_files]
df = pd.concat(df_list, ignore_index=True)

# 筛选出湖北省的数据
df =df[(df['province'] == '湖北省') & (df['city'].isna())]

# 筛选日期
# 从2020-01-20到2020-03-13的数据
df['date'] = pd.to_datetime(df['date'])
start_date = '2020-01-20'
end_date = '2020-03-13'
df = df[(df['date'] >= start_date) & (df['date'] <= end_date)]
df = df.reset_index(drop=True)

# 处理后的数据
display(df[['date', 'confirmed']])
处理后的数据：
date confirmed
0 2020-01-20 270
1 2020-01-21 375
2 2020-01-22 444
3 2020-01-23 549
4 2020-01-24 729
5 2020-01-25 1052
6 2020-01-26 1423
7 2020-01-27 2714
8 2020-01-28 3554
9 2020-01-29 4586
10 2020-01-30 5806
11 2020-01-31 7153
12 2020-02-01 9074
13 2020-02-02 11177
14 2020-02-03 13522
15 2020-02-04 16678
16 2020-02-05 19665
17 2020-02-06 22112
18 2020-02-07 24953
19 2020-02-08 27013
20 2020-02-09 29631
21 2020-02-10 31728
22 2020-02-11 33366
23 2020-02-12 47163
24 2020-02-13 51986
25 2020-02-14 54406
26 2020-02-15 56249
27 2020-02-16 58182
28 2020-02-17 59989
29 2020-02-18 61682
30 2020-02-19 62457
31 2020-02-20 63088
32 2020-02-21 63454
33 2020-02-22 63889
34 2020-02-23 64287
35 2020-02-24 64786
36 2020-02-25 65187
37 2020-02-26 65596
38 2020-02-27 65914
39 2020-02-28 66337
40 2020-02-29 66907
41 2020-03-01 67103
42 2020-03-02 67217
43 2020-03-03 67332
44 2020-03-04 67466
45 2020-03-05 67592
46 2020-03-06 67666
47 2020-03-07 67707
48 2020-03-08 67743
49 2020-03-09 67760
50 2020-03-10 67773
51 2020-03-11 67781
52 2020-03-12 67786
53 2020-03-13 67790

模型建构与分析

使用 scipy.optimize 模块中的 curve_fit() 函数对逻辑斯蒂模型进行参数估计。该函数的基础是最小二乘法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# 获取时间变量t的取值和累计确诊人数P(t)的取值
t_values = df.index.to_numpy()
P_values = df['confirmed'].to_numpy()

from scipy.optimize import curve_fit

# 定义逻辑斯蒂函数
def logistic_function(t, K, r, P0):
    """
    t: 时间序列
    K: 最大感染人数
    r: 感染率
    P0: 初始感染人数
    """
    return K * P0 * np.exp(r * t) / (K + P0 * (np.exp(r * t) - 1))

# 定义逻辑斯蒂微分函数
def logistis_differential(t, K, r, P0):
    return r * K * P0 * np.exp(r * t) * (K - P0) / (K + P0 * np.exp(r * t) - P0)**2

# Parameters Optimal -> popt
# Parameters Covariance -> pcov
popt, pcov = curve_fit(logistic_function, t_values, P_values)

# 获取拟合参数
K, r, P0 = popt
print(f"拟合参数: K={K}, r={r}, P0={P0}")

拟合参数: K=67665.19885599917, r=0.24185228081234944, P0=498.19314823490566

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from matplotlib import rcParams
import matplotlib.pyplot as plt
import matplotlib.dates as mdates

# 设置以使中文字体正常显示于图表中
rcParams['font.family'] = 'SimHei'

# 创建日期范围，用dates代替t_values
dates = pd.date_range(start=start_date, periods=len(t_values), freq='D')

# 可视化拟合结果
plt.figure(figsize=(10, 6))
plt.scatter(dates, P_values, label="实际值", color="blue")
plt.plot(dates, logistic_function(t_values, *popt), label="拟合值", color="red")
plt.xlabel("日期")
plt.ylabel("累计确诊人数")
# 设置x轴日期格式
plt.gca().xaxis.set_major_formatter(mdates.DateFormatter('%Y-%m-%d'))
plt.gca().xaxis.set_major_locator(mdates.WeekdayLocator())  # 每周显示一个日期
plt.gcf().autofmt_xdate()  # 自动旋转日期标签，使其更清晰
plt.legend()
plt.show()
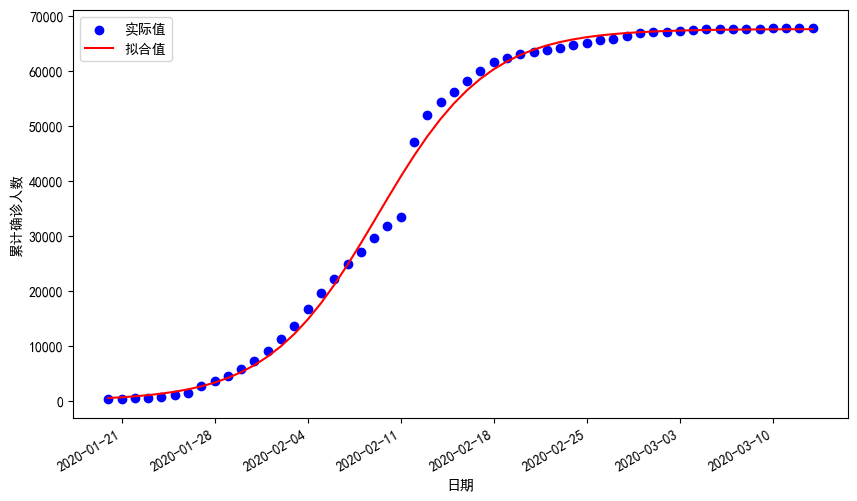
result

小结

从最终的图表可以看出，数据拟合结果与逻辑斯蒂函数相符，表明COVID-19传播的趋势符合该模型的预期。通过图表可以观察到，到了2020年3月初，病毒的传播速度开始放缓，传播曲线趋于平稳，显示出疫情在此时已接近传播的上限。