几何光学
几何光学
几何光学(Geometrical optics, ray optics),是将光视作光线(ray),以研究光的传播特性的光学模型。
几何光学不考虑某些光学特性,比如光的波动性。另外,本文只涉及平面几何,图例均使用PhyDemo制作。本文在研究物像大小关系时,只考虑高度的缩放。
几何光学三定律
1. 光的直线传播定律(The law of rectilinear propagation)
在同一均匀介质中,光沿直线传播。
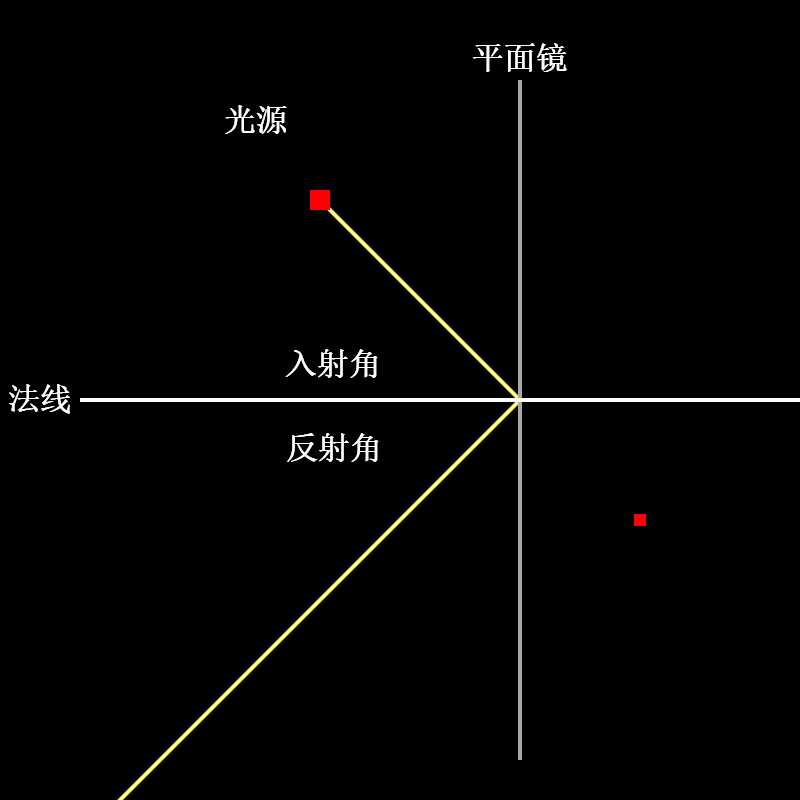
2. 光的反射定律(The law of reflection)
当光遇到物体表面时,会发生反射。此时:
入射光线、反射光线和法线处于同一平面
反射角等于入射角
示意图如下:
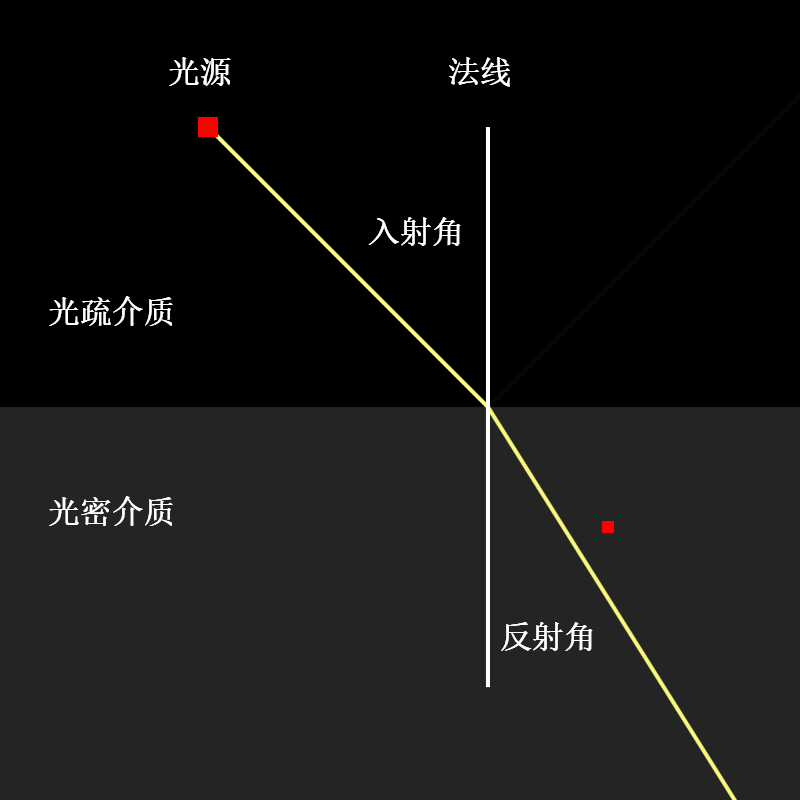
3. 光的折射定律(The law of refraction) / 斯涅尔定律(Snell’s Law)
当光穿过不同介质之间的表面时,会发生折射。此时:
入射光线、折射光线和法线处于同一平面
如果第一种介质和第二种介质的折射率分别为\(n_1,n_2\),入射光线、折射光线分别与法线形成的角为\(\theta_1,\theta_2\),那么\(n_1\sin{\theta_1} = n_2\sin{\theta_2}\)
折射率从其名字理解指,如果折射率越大,那么折射光线偏离入射光线的角度会变得更大,意味着光线被“弯折”的程度越大。从定义出发理解,折射率\(n=c/v\),其中\(c\)指光在真空中的传播速度,此为不变量,\(v\)指光在介质中的传播速度,所以\(n\)也可以理解为介质对光传播的“阻力”,于是\(n\)值较小的介质被称作光疏介质,\(n\)值较大的介质被称作光密介质。
示意图如下:
经典模型
正负号的约定
当物(object)与入射光线(incoming)处于同一侧时,物距\(s>0\)。
当像(image)与反射或折射光线(outcoming)处于同一侧时,像距\(s'>0\)。
当圆心与反射或折射光线(outcoming)处于同一侧时,曲率\(R>0\)。
当焦点(focal point)与反射或折射光线(outcoming)处于同一侧时,焦距\(f>0\)。
取物的高度为\(y>0\),则当像为实像(real)时,像的高度\(y'<0\);当像为虚像(virtual)时,像的高度\(y'>0\)。
球面反射模型
凹面镜的物像关系
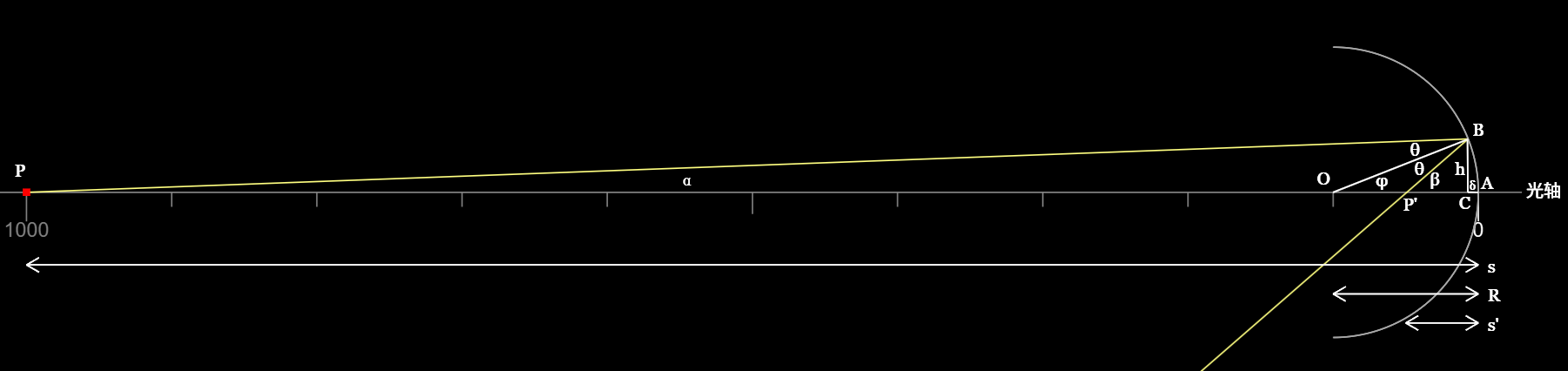
如图所示。空间中有一光源\(P\)和一圆心位于点\(O\)的凹透镜。连接\(PO\)并延长,使其与凹透镜相交于点\(A\);直线$ PA \(被称为光轴,点\)A\(被称为顶点。从光源\)P\(引出一条光线与凹透镜相交于点\)B\(,连接\)BO\(。入射光线在点\)B\(处发生反射,反射光线\)BP’\(与光轴相交于点\)P’\(,显然\)PBO = OBP’\(。过点\)B\(作\)BC\(垂直于\)PA\(,垂足为点\)C$。
令$ = APB, = AP’B,= AOB, = PBO = OBP’\(;\ 令\)s=AP,s’=AP’,R=AO=OB,h=BC,=AC$。
在进行分析前,请注意我们在此研究的球面反射模型的对象只涉及近轴光线。此时\(s\)远大于\(R\),\(\alpha\)接近于\(0\)(体现为示例图的宽度远大于高度)。
根据几何原本第1卷第32命题,三角形一外角等于不相邻两内角之和,有
\[ \begin{aligned} \phi &= \alpha + \theta \\ \beta &= \phi + \theta \end{aligned} \]
化简上式得
\[ \begin{equation} \alpha + \beta = 2\phi \end{equation} \tag{1.1} \]
根据三角函数的定义,有
\[ \begin{equation} \begin{aligned} \tan{\alpha} &= \frac{h}{s-\delta} \\ \tan{\beta} &= \frac{h}{s'-\delta} \\ \tan{\phi} &= \frac{h}{R-\delta} \\ \end{aligned} \end{equation} \tag{1.2} \]
在继续进行分析之前,我们会用到一个粗略的结论:当角度$\(非常小时,\) \(;也就是说\)\(和\)$等价无穷小,显然这是可行的,因为
\[ \lim_{\theta \to 0} \frac{\tan\theta}{\theta} = 1 \]
当\(\alpha\)非常小时,\(\beta,\phi,\delta\)也非常小,结合$ $,于是我们得到近似结果
\[ \begin{equation} \begin{aligned} \alpha &= \frac{h}{s} \\ \beta &= \frac{h}{s'} \\ \phi &= \frac{h}{R} \\ \end{aligned} \end{equation} \tag{1.3} \]
联立\((1.1)(1.3)\),我们得到了凹面镜反射的物距、像距与曲率之间的关系。
\[ \begin{equation} \frac{1}{s} + \frac{1}{s'} = \frac{2}{R} \end{equation} \tag{1.4} \]
凸面镜的物像关系
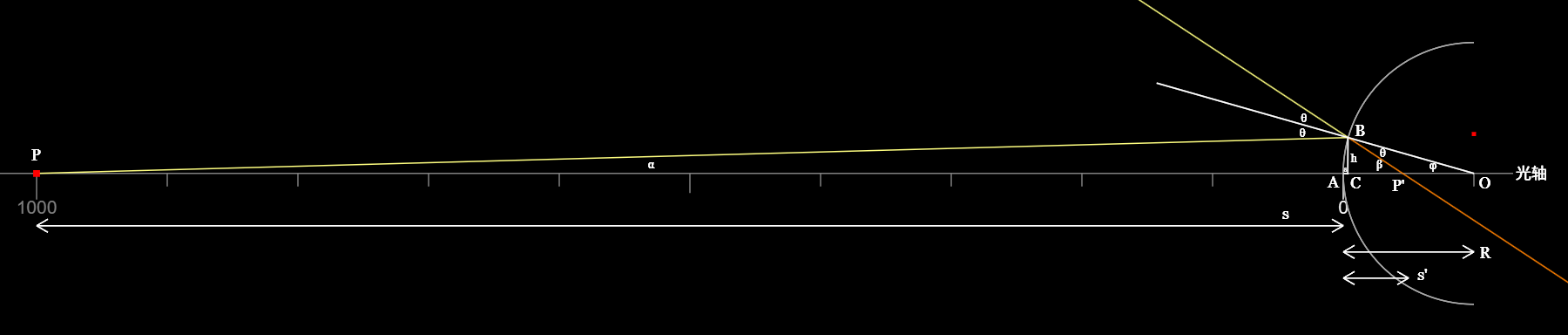
凸面镜的情况凹面镜的类似。不同在于,凸面镜的情况时,\(s'<0,R<0\)。
根据几何原本第1卷第32命题,三角形一外角等于不相邻两内角之和,有
\[ \begin{aligned} \alpha + \beta &= 2\theta \\ \alpha + \phi &= \theta \\ \end{aligned} \]
化简上式得
\[ \begin{equation} \alpha - \beta = - 2\phi \end{equation} \tag{2.1} \]
因为\(s'<0,R<0\),所以要先对二者取绝对值,再计算\(\tan\)函数
\[ \begin{equation} \begin{aligned} \tan{\alpha} &= \frac{h}{s+\delta} \\ \tan{\beta} &= \frac{h}{|s'|+\delta} &= \frac{h}{-s'+\delta} \\ \tan{\phi} &= \frac{h}{|R|+\delta} &= \frac{h}{-R+\delta} \\ \end{aligned} \end{equation} \tag{2.2} \]
就像我们在凹面镜处理的方法一样,取\((2.2)\)的近似
\[ \begin{equation} \begin{aligned} \alpha &= \frac{h}{s} \\ \beta &= -\frac{h}{s'} \\ \phi &= -\frac{h}{R} \end{aligned} \end{equation} \tag{2.3} \]
联立\((2.2)(2.3)\),我们得到了凸面镜的物像关系,其与凹透镜的物象关系相同
\[ \begin{equation} \frac{1}{s} + \frac{1}{s'} = \frac{2}{R} \end{equation} \tag{2.4} \]
焦点与焦距
现在,我们有了球面反射公式\((1.4)\)和\((2.4)\)。当物离镜面非常远时(即\(s=\infty\)时),所有的光线互相平行,此时
\[ \begin{aligned} \frac{1}{\infty} + \frac{1}{s'} &= \frac{2}{R} \\ s' &= \frac{R}{2} \end{aligned} \]
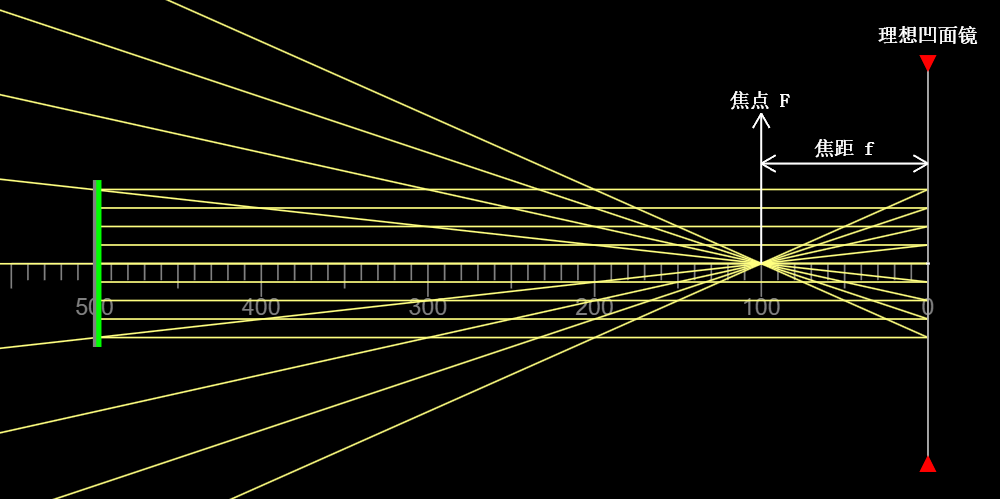
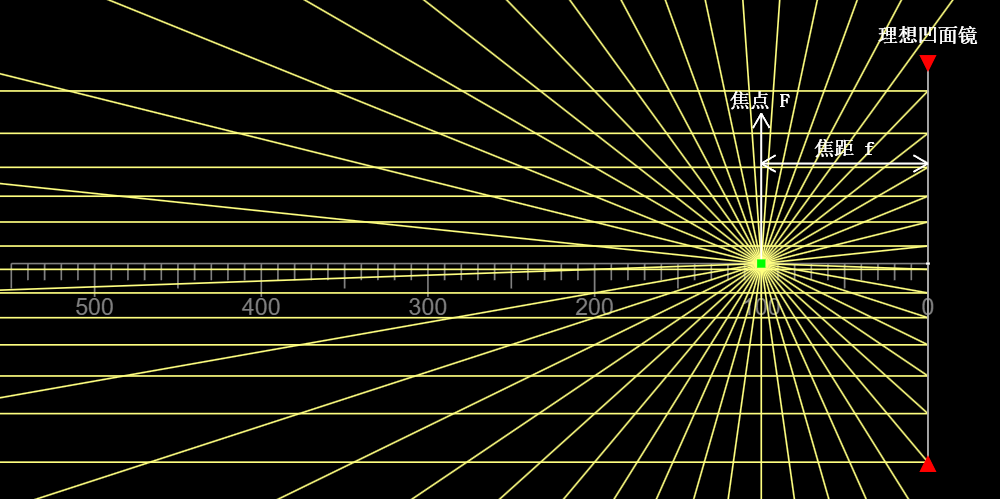
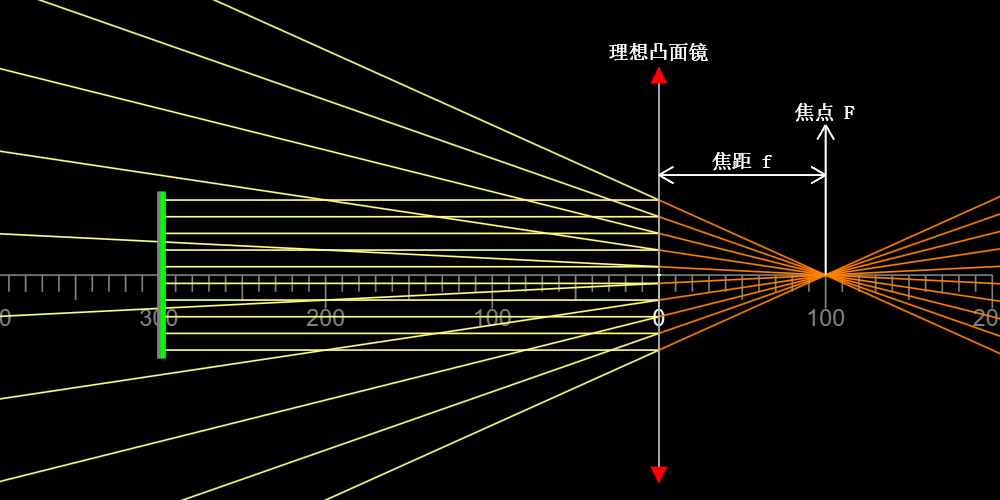
如图所示,在这种情况下,所有入射的平行光线均会汇聚在点\(F\)上。点\(F\)被称作焦点,顶点到焦点的距离被称作焦距\(f\)。
取\(f=R/2\),我们便得到了更常见的球面反射的物像公式:
\[ \begin{equation} \begin{aligned} \frac{1}{s} + \frac{1}{s'} &= \frac{1}{f} \\ \end{aligned} \end{equation} \tag{3.1 球面反射的物像公式} \]
延展物体在球面镜中的成像
凹面镜成像
延展物体位于焦点之外
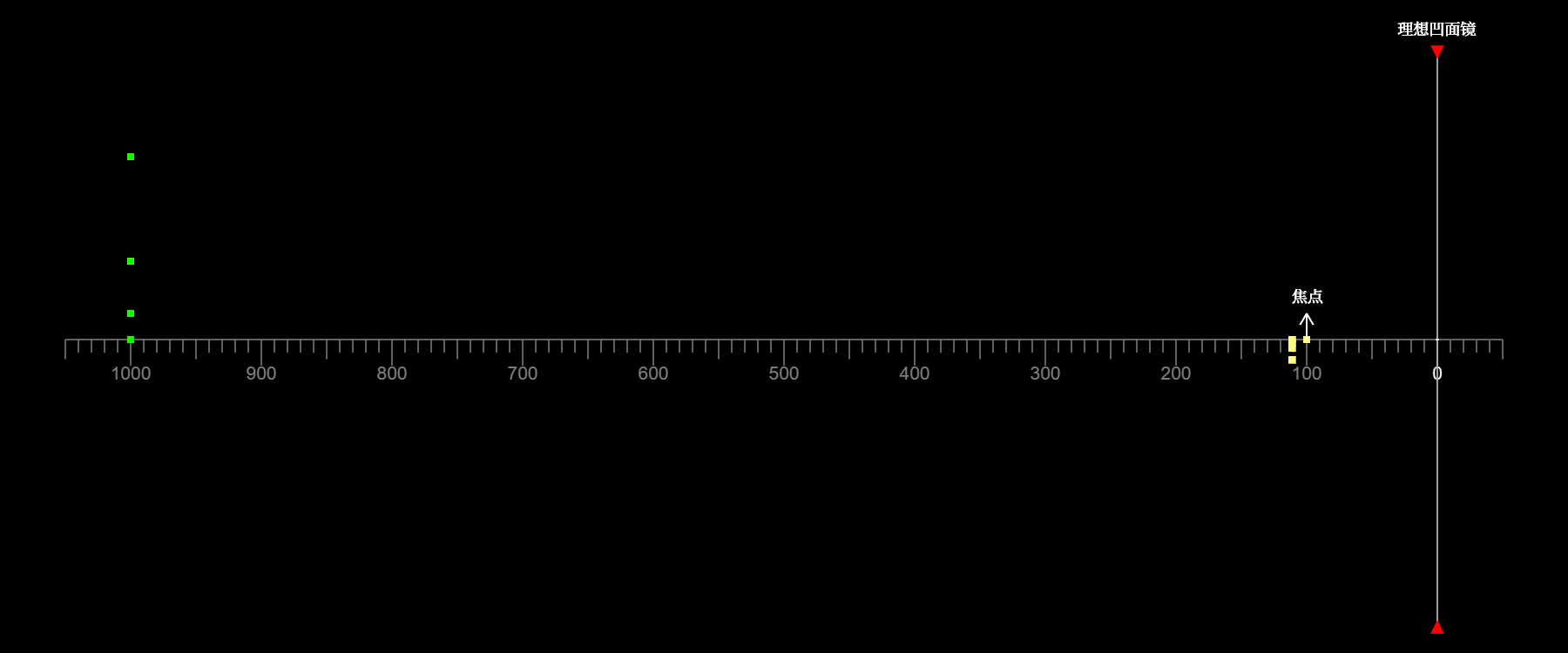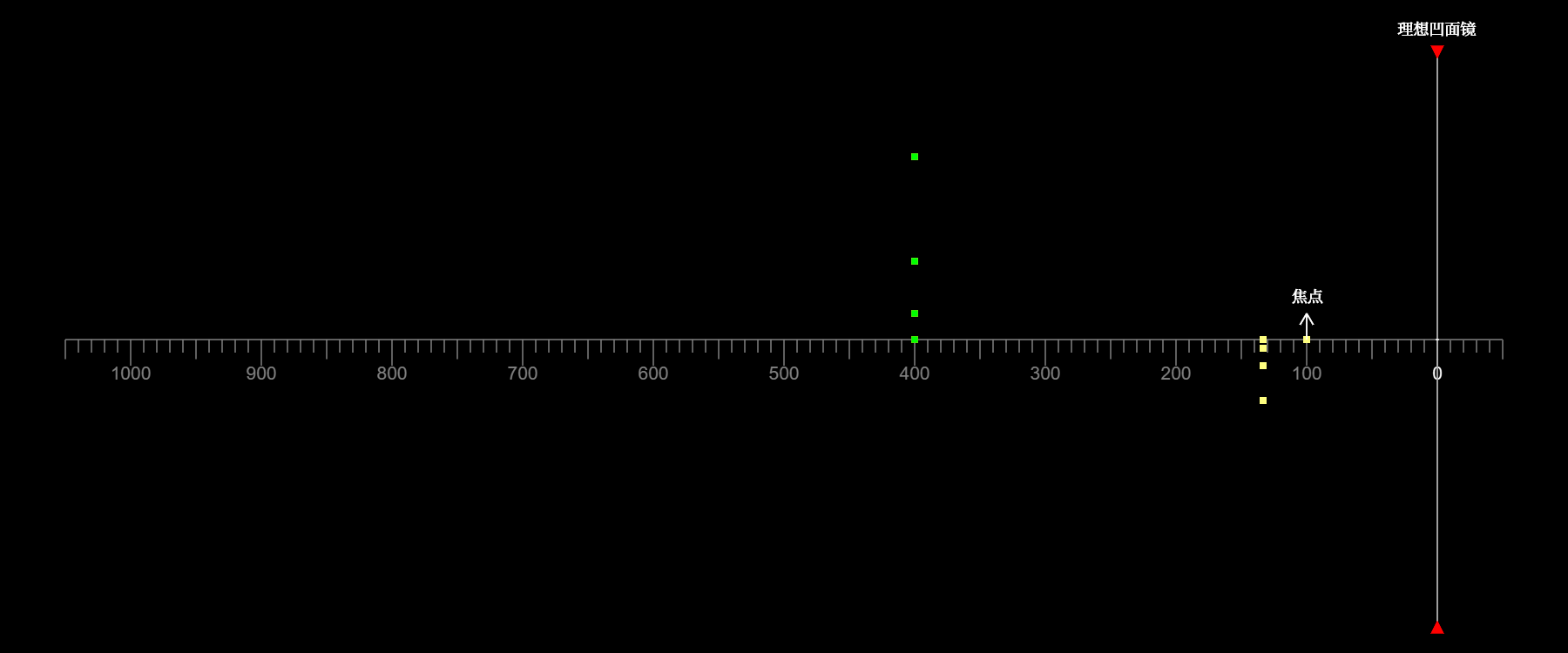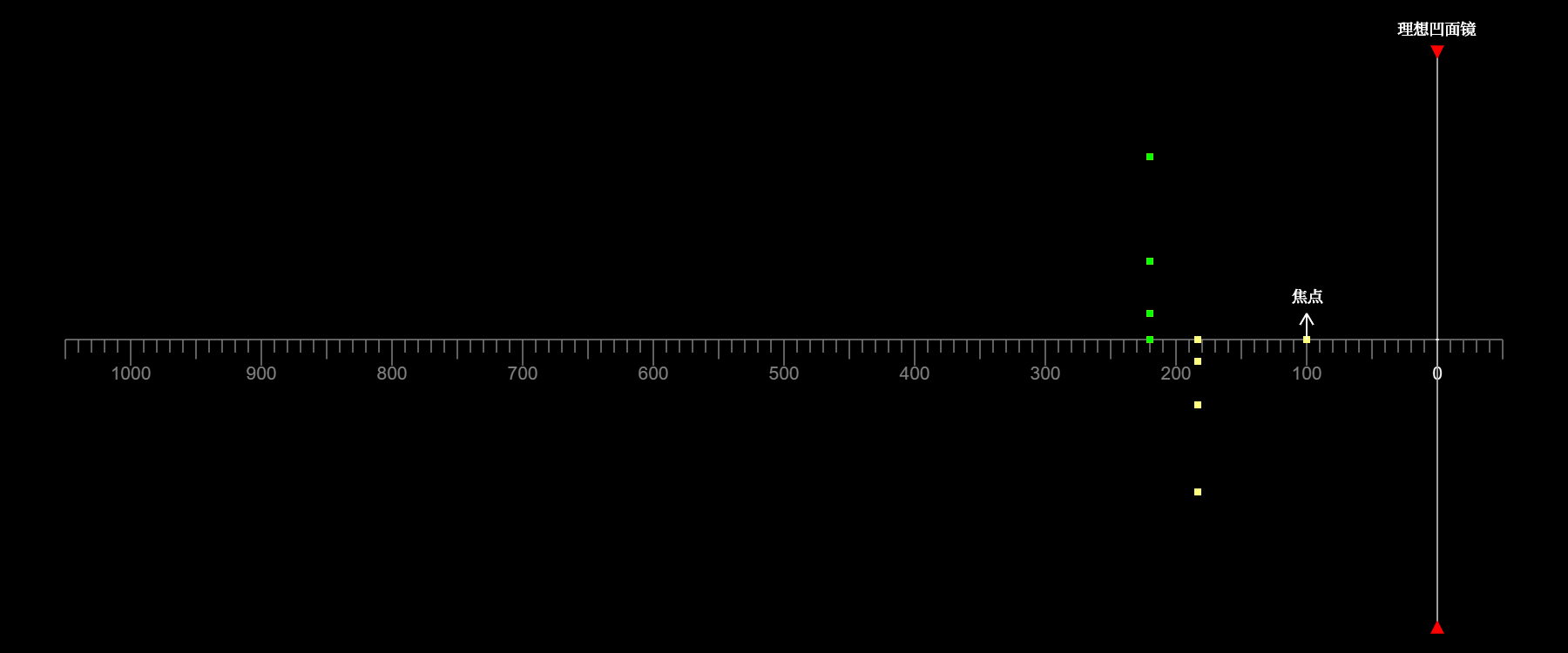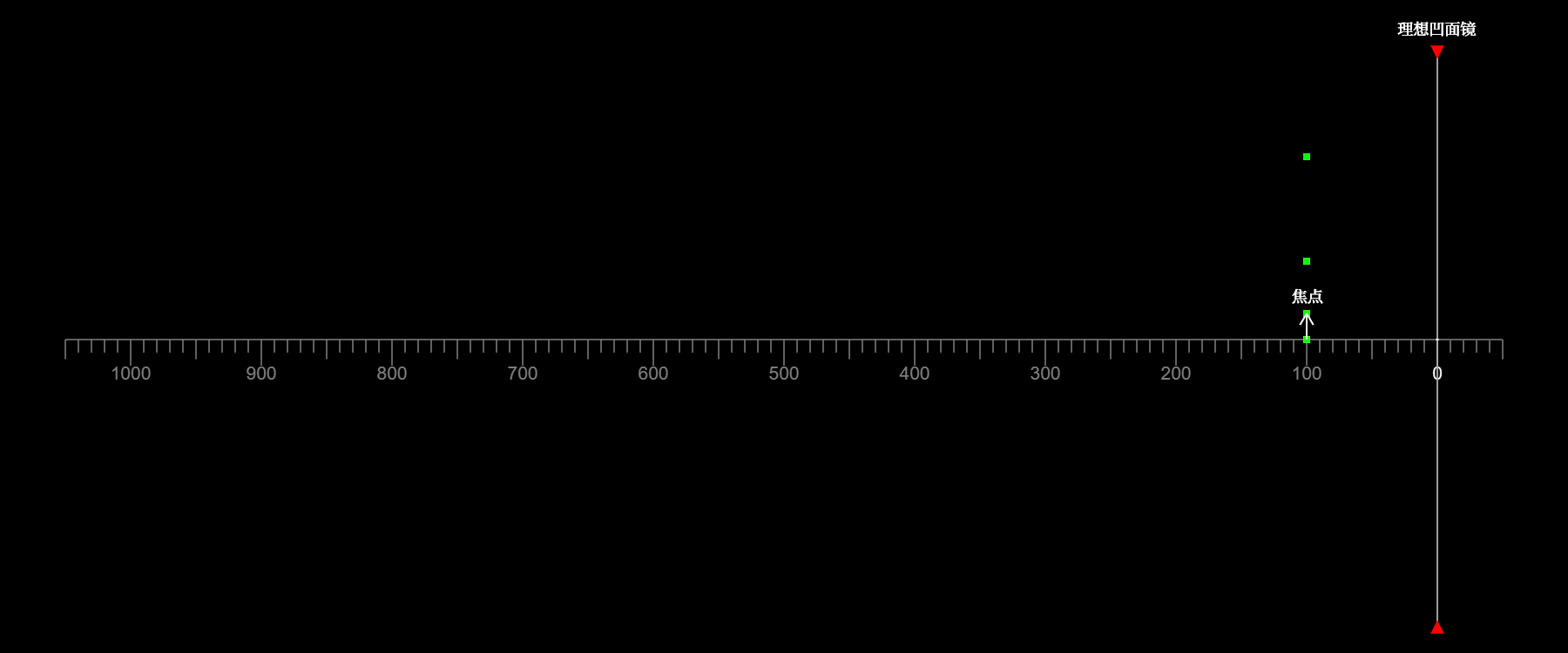
如图所示,绿点代表物,黄点代表像。当延展物体位于焦点之外时
像为实像,物和像上下颠倒
当物位于圆心之外时,物的高度大于像的;当物位于圆心之上时,物的高度等于像的;当物位于圆心之内时,物的高度小于像的
截取其中一帧进行分析
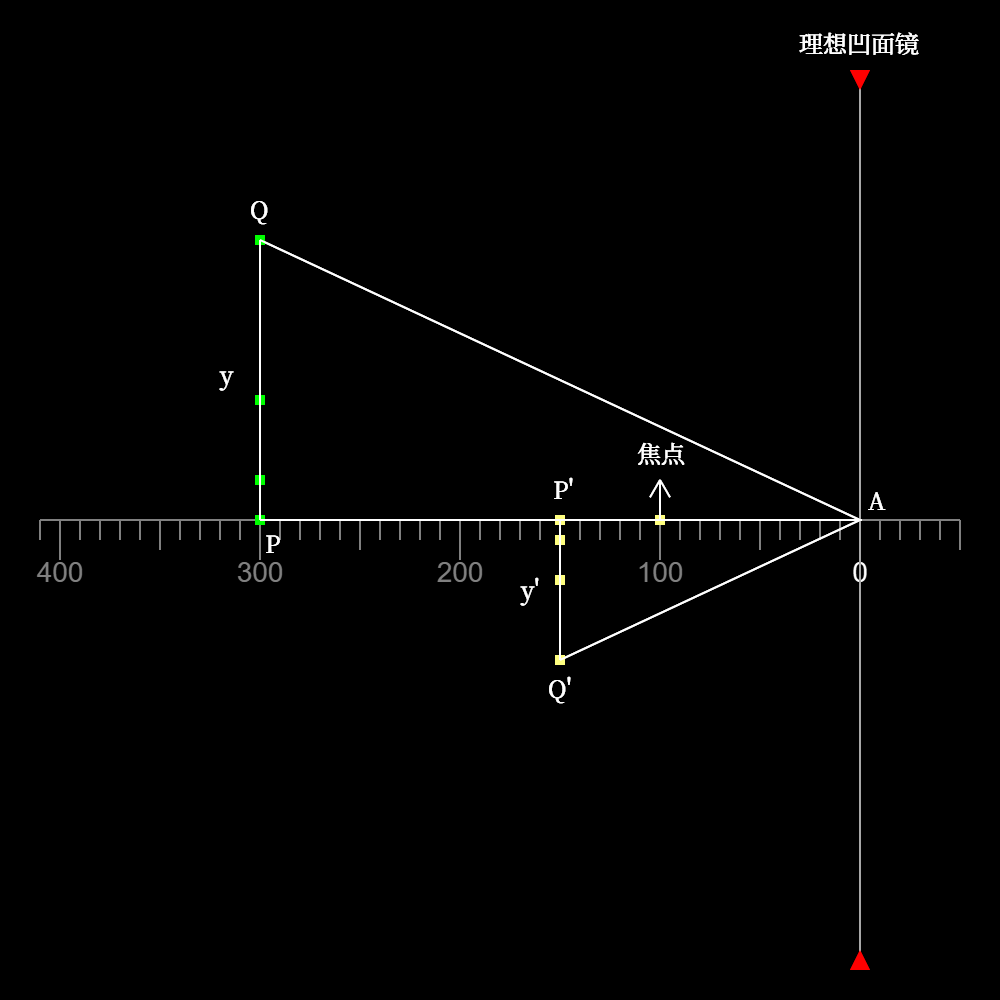
如图所示,\(PQ\)代表延展物体,令\(y=PQ\);\(P'Q'\)代表延展物体的像,令\(y'=-P'Q'\)(物与像上下颠倒);物距\(s=AP\),像距\(s=AP'\)。
注意到,\(\triangle APQ\)与\(\triangle Ap'Q'\)互为相似三角形,所以
\[ \frac{PQ}{P'Q'} = \frac{AP}{AP'} \]
又因为
\[ \frac{PQ}{P'Q'} = \frac{-y'}{y} ,\ \frac{AP}{AP'} = \frac{s'}{s} \]
所以
\[ \frac{-y'}{y} = \frac{s'}{s} \]
我们定义\(y'/y\)为侧向放大率(lateral magnification),用符号\(m\)表示,那么
\[ \begin{equation} m = \frac{y'}{y} = - \frac{s'}{s} \end{equation} \tag{3.2} \]
延展物体位于焦点之上
当延展物体位于焦点之上时,物距\(s=f\),根据\((3.1)\)可知
\[ \frac{1}{f} + \frac{1}{s'} = \frac{1}{f} \]
所以\(s' = \infty\)。此时像在无穷远处。
根据\((3.2)\)可知
\[ m = -\frac{\infty}{f}=- \infty \]
所以此时像无穷大。
具体来说,当延展物体位于焦点之上时,凹面镜中无法形成清晰的像,而是一种“混沌”的像,并且整个凹面镜的内容都被这个“混沌”的像所填满。
可以参考下图(截取自YouTube视频Concave
Mirror Demo: Pendulum):

延展物体位于焦点之内
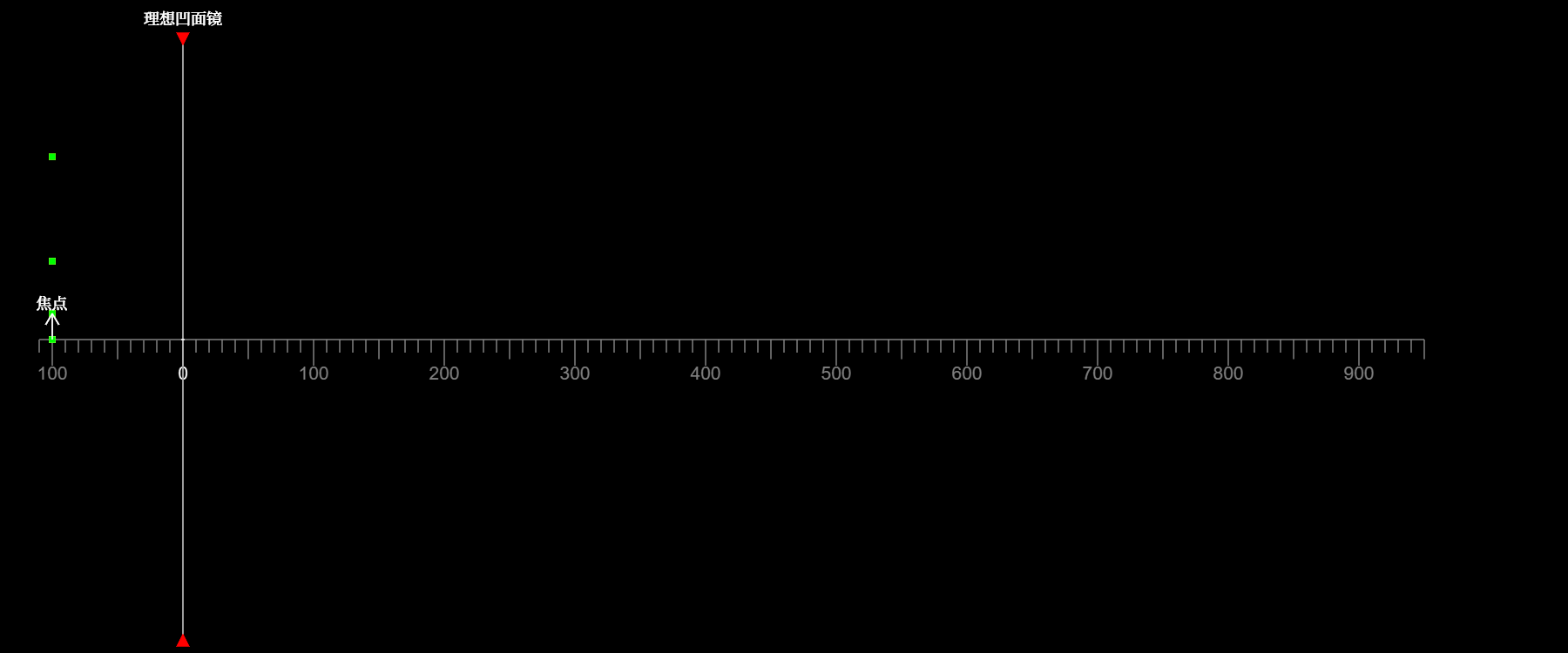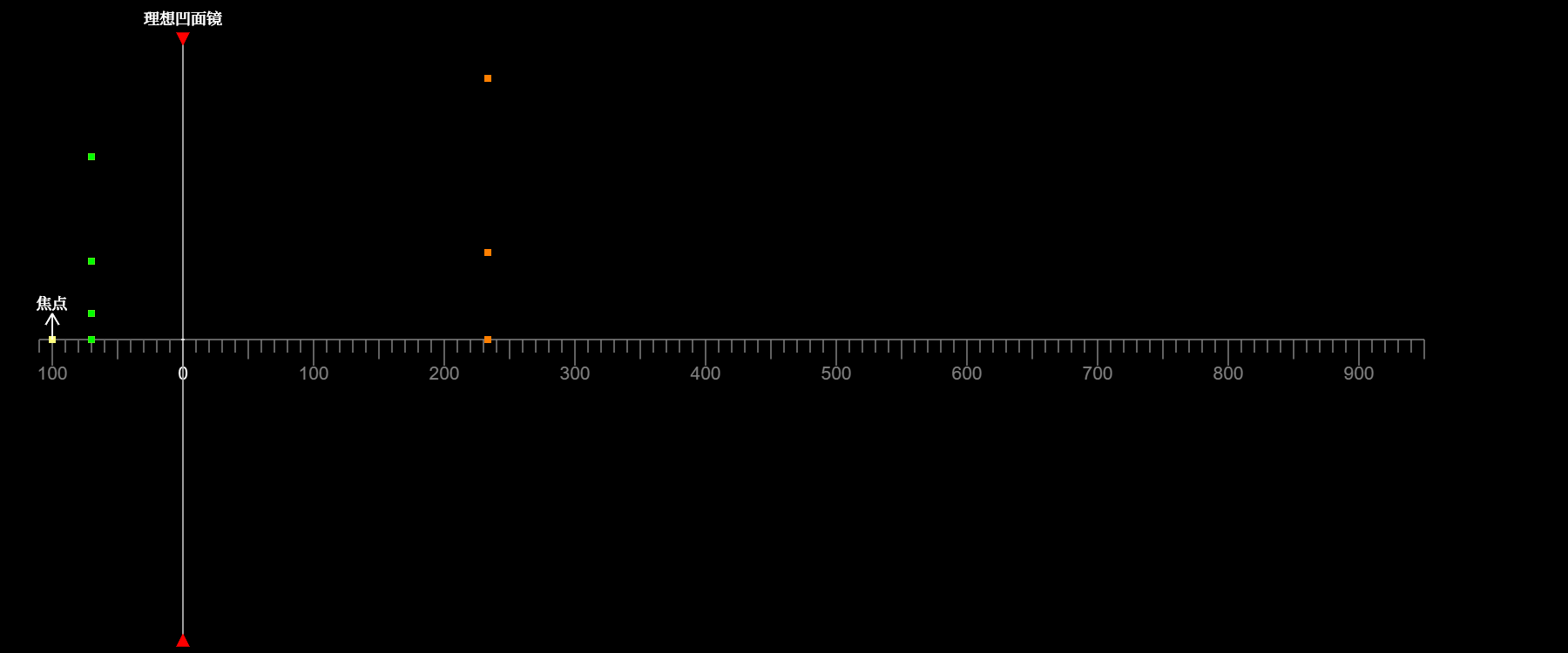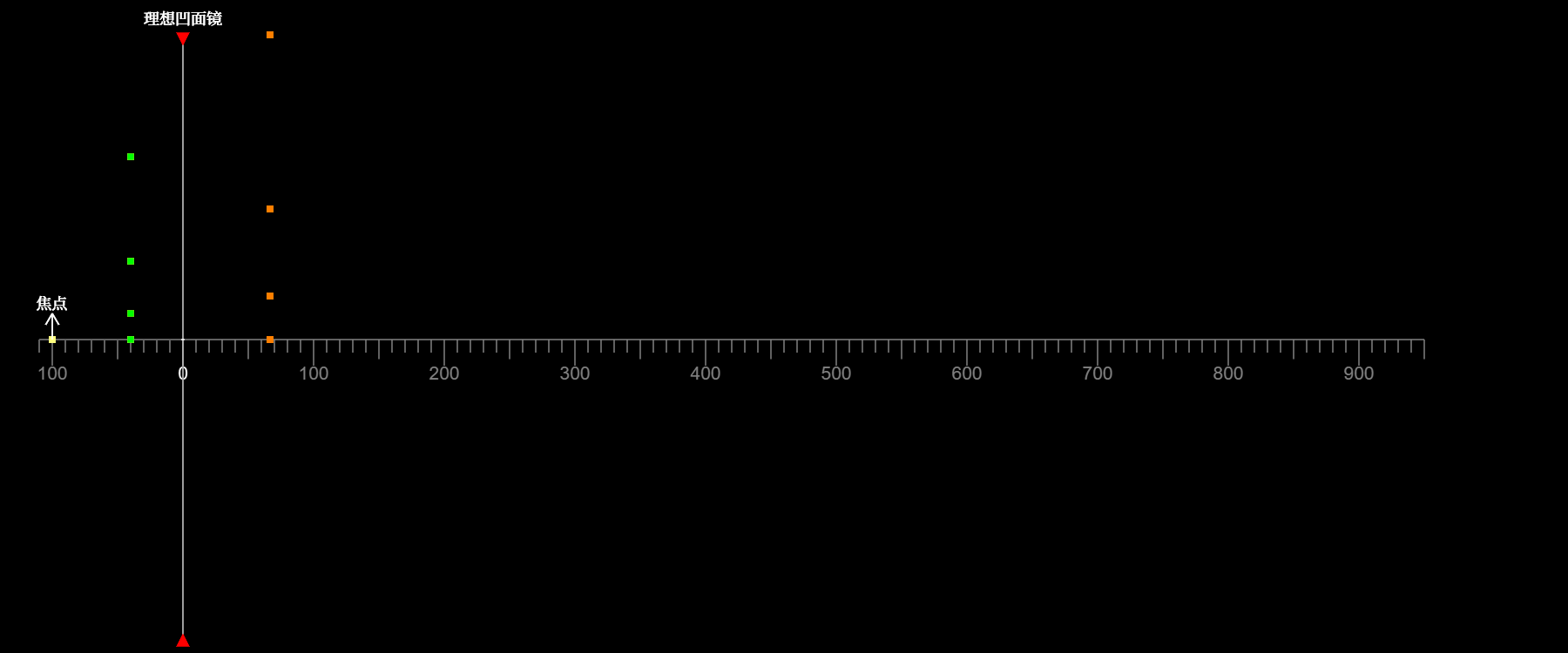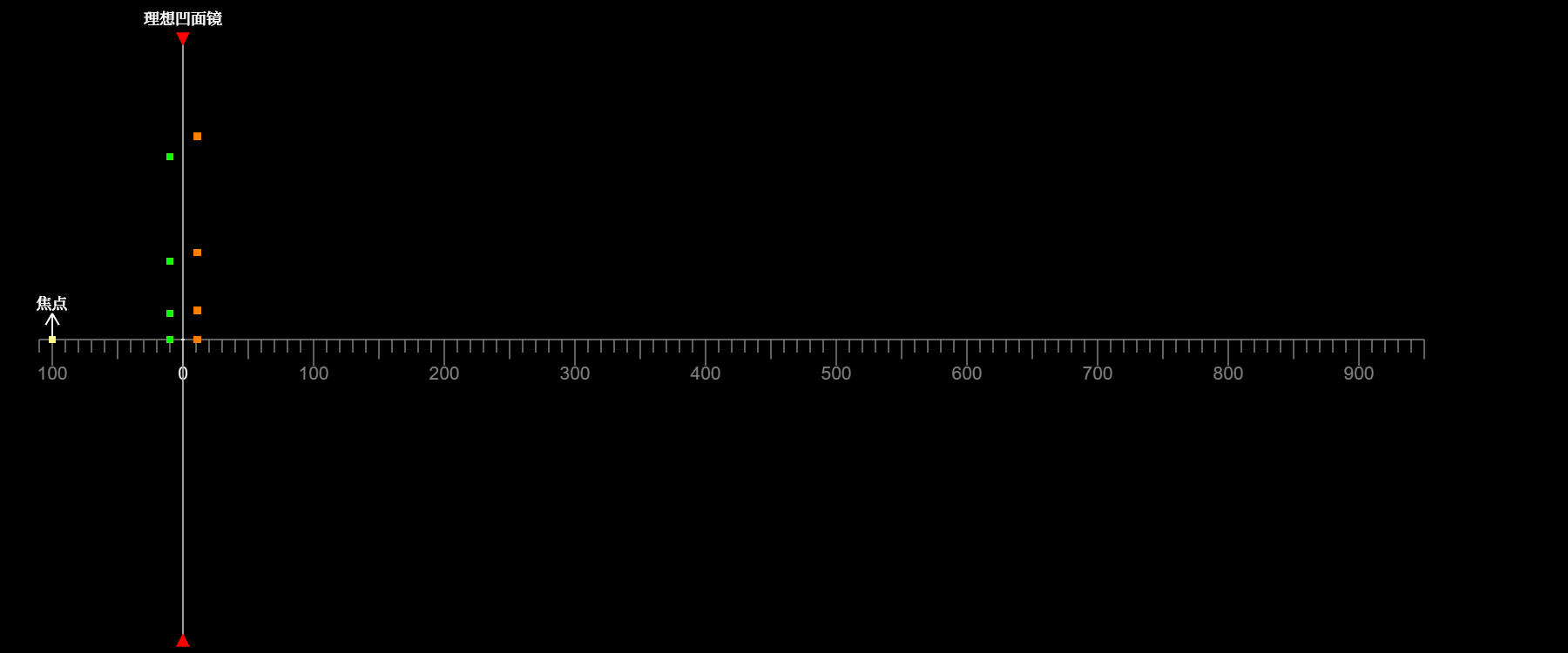
如图所示,绿点代表物,橙点代表像。当延展物体位于焦点之内时
像为虚像,物和像上下方向相同
像的高度始终大于物的
截取其中一帧进行分析
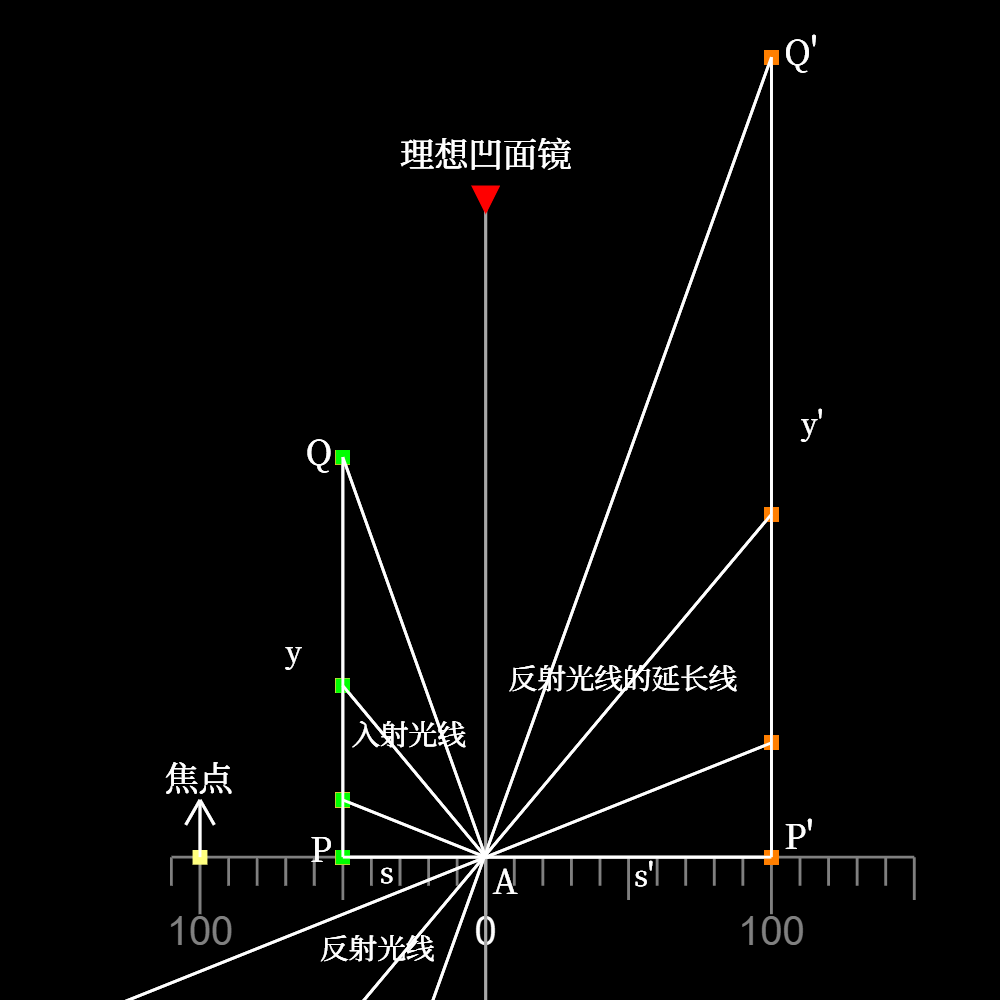
如图所示,\(PQ\)代表延展物体,令\(y=PQ\);\(P'Q'\)代表延展物体的像,令\(y'=P'Q'\);物距\(s=AP\),像距\(s=-AP'\)(像与反射光线不同侧)。
注意到,\(\triangle APQ\)与\(\triangle Ap'Q'\)互为相似三角形,所以
\[ \frac{PQ}{P'Q'} = \frac{AP}{AP'} \]
又因为
\[ \frac{PQ}{P'Q'} = \frac{y'}{y} ,\ \frac{AP}{AP'} = \frac{-s'}{s} \]
所以
\[ \frac{y'}{y} = -\frac{s'}{s} \]
我们定义\(y'/y\)为侧向放大率(lateral magnification),用符号\(m\)表示,那么
\[ \begin{equation} m = \frac{y'}{y} = - \frac{s'}{s} \end{equation} \tag{3.3} \]
凸面镜成像
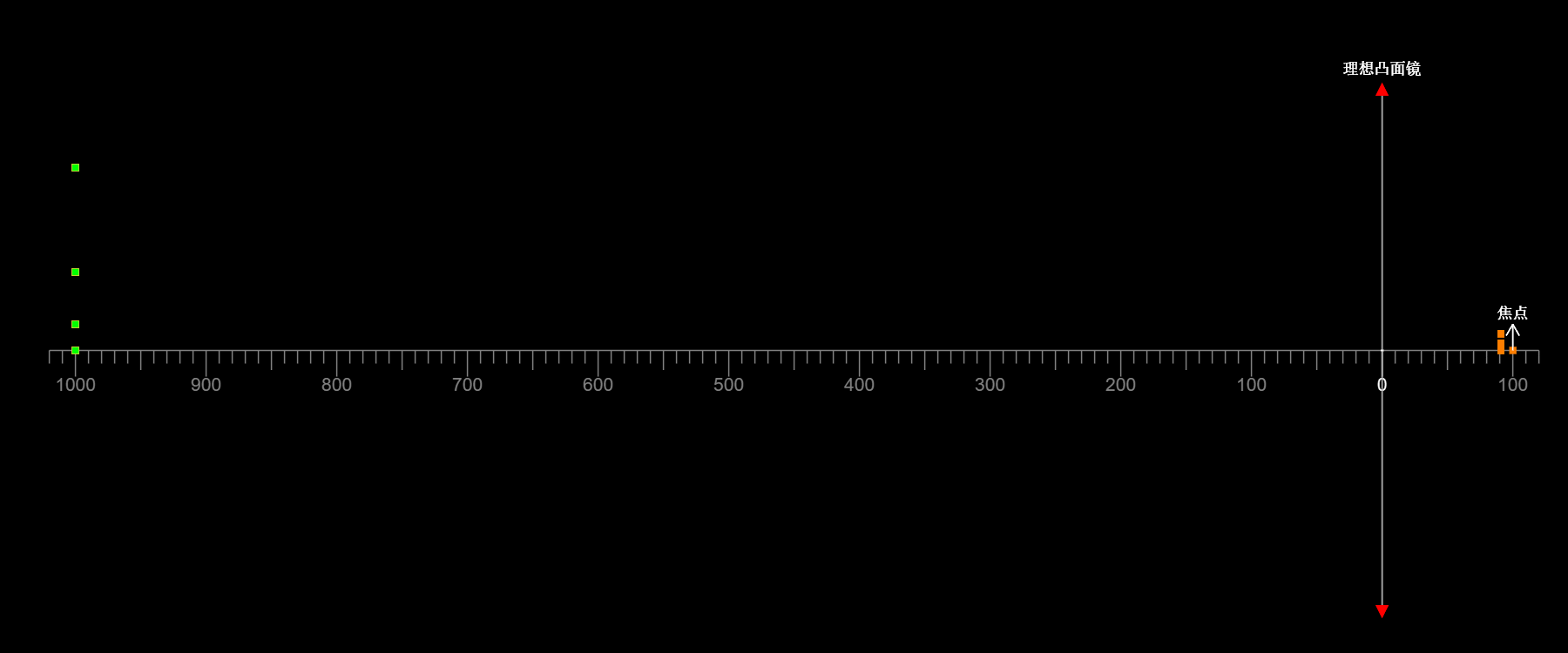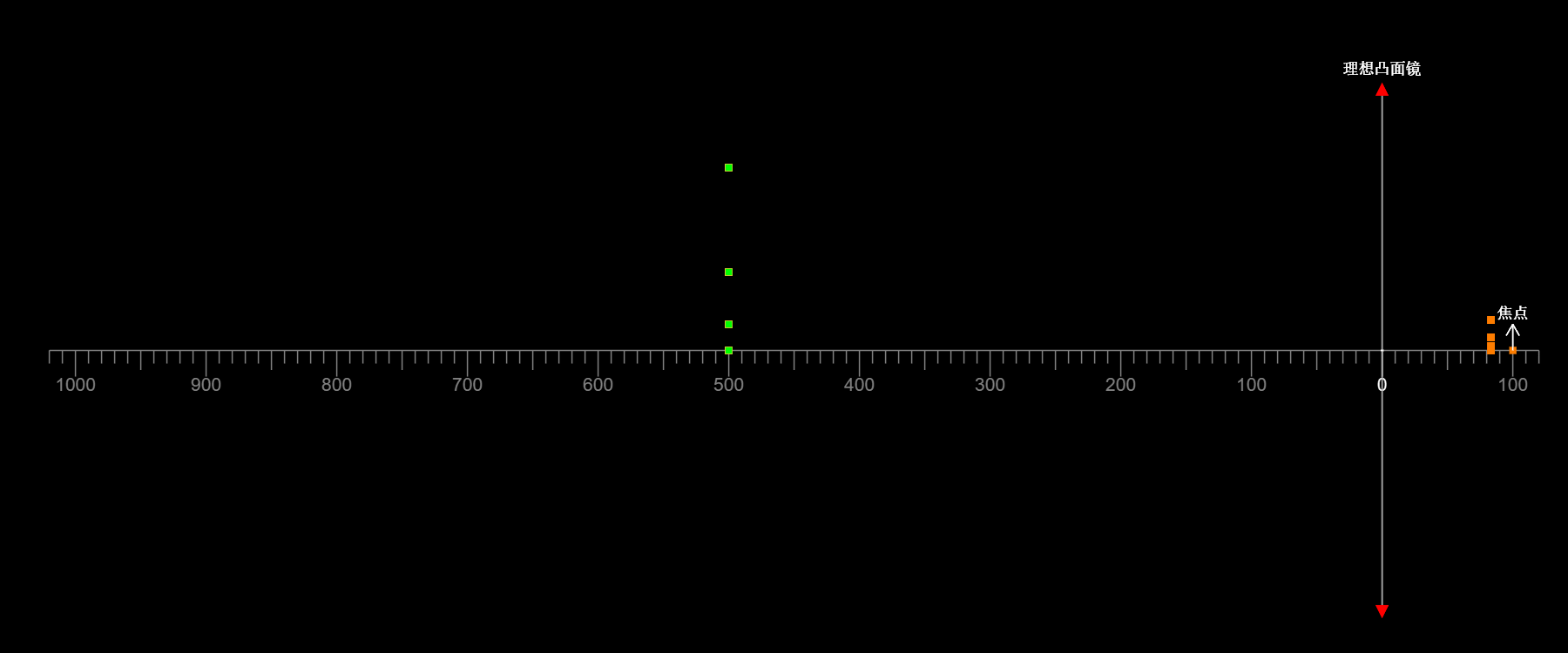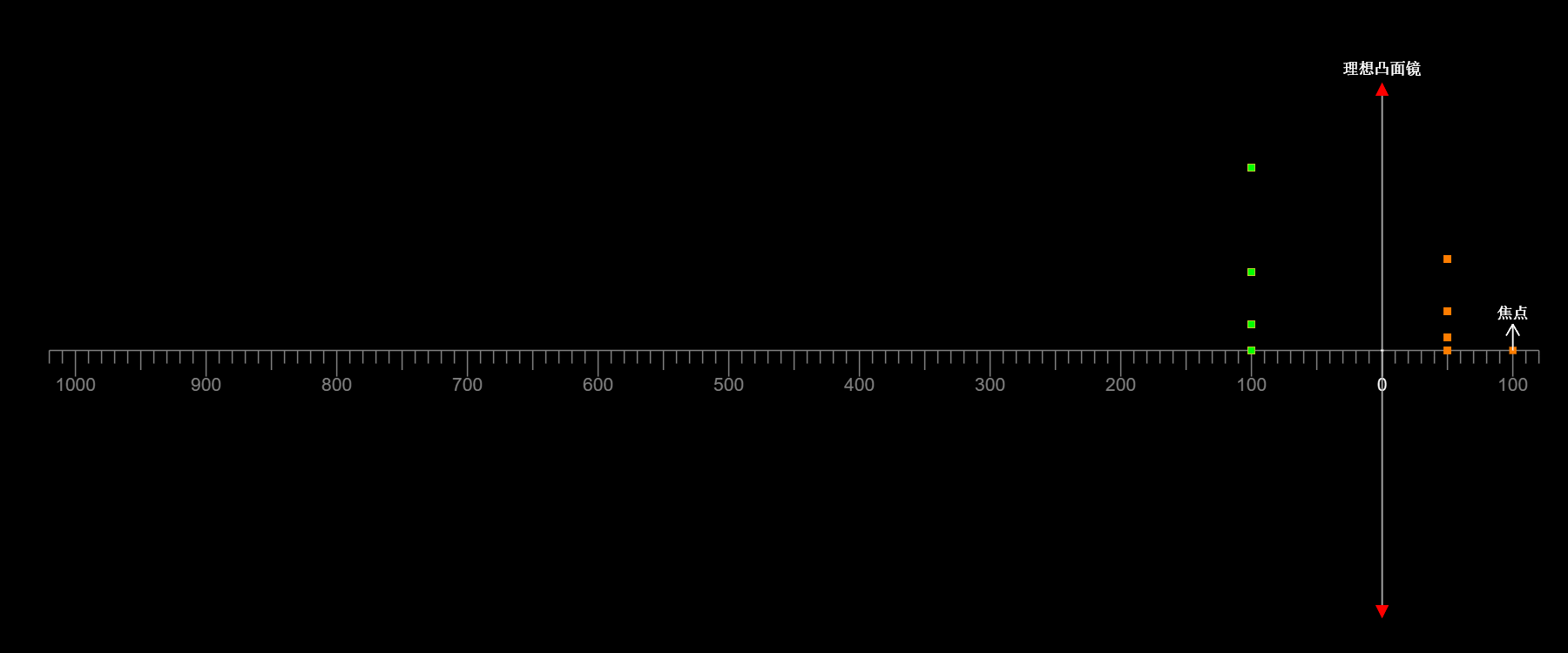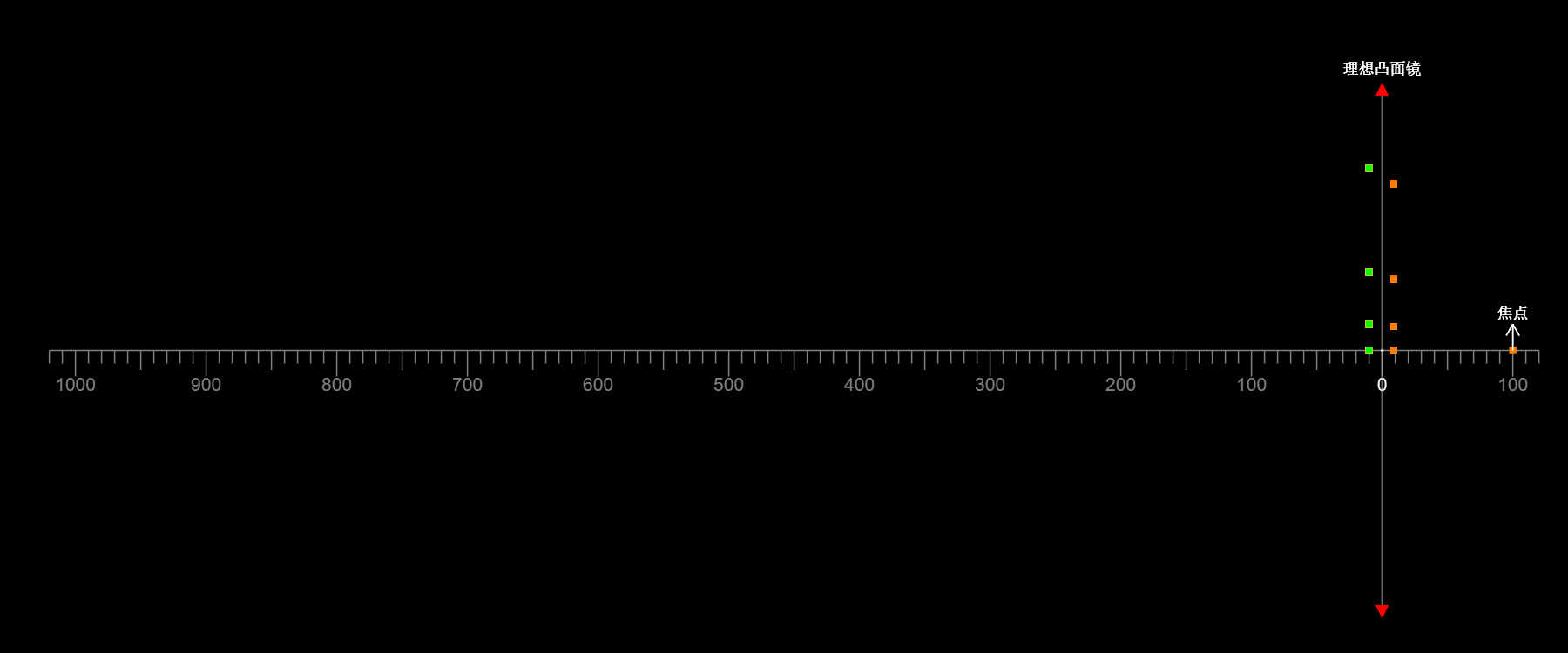
如图,在凸面镜成像过程中,无论物离镜面是远是近
像始终是虚像,物与像的高度始终同向
像的高度始终小于物的
截取其中一帧进行分析
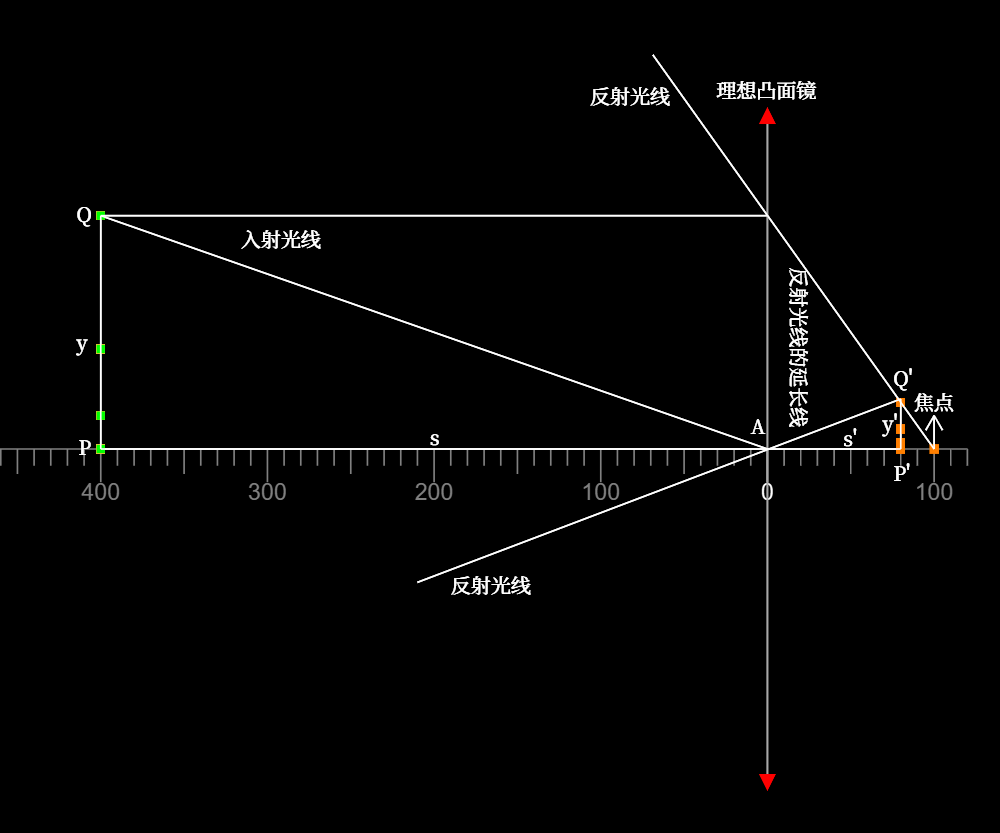
如图所示,\(PQ\)代表延展物体,令\(y=PQ\);\(P'Q'\)代表延展物体的像,令\(y'=P'Q'\);物距\(s=AP\),像距\(s=-AP'\)(像与反射光线不同侧)。
与凹面镜成像的延展物体位于焦点之内的分析类似,这两种情况就像是将物与像的位置交换了一般。我们最终也能得到公式\((3.3)\)。
球面折射模型
凸面折射

如图,一光线从光疏介质射入光密介质内,两个介质的交界面凸起,其曲率半径为\(R\)。
物距\(s=AP\),像距\(s'=AP'\),曲率\(R=AO\)。
入射角为\(\theta_1\),折射角为\(\theta_2\)。
\(\alpha = \angle APB, \beta=\angle AP'B,
\phi = \angle AOB\)。
\(h=BC, \delta = AC\)。
根据折射定律,得
\[ \begin{equation} n_1 \sin{\theta_1} = n_2 \sin{\theta_2} \end{equation} \tag{4.1} \]
根据三角形内角与外角的关系,得
\[ \begin{equation} \begin{aligned} \theta_1 &= \alpha + \phi \\ \theta_2 &= \phi - \beta \end{aligned} \end{equation} \tag{4.2} \]
根据\(\tan\)函数的定义,得
\[ \begin{equation} \begin{aligned} \tan{\alpha} &= \frac{h}{s + \delta} \\ \tan{\beta} &= \frac{h}{s' - \delta} \\ \tan{\phi} &= \frac{h}{R - \delta} \end{aligned} \end{equation} \tag{4.3} \]
我们希望找到一个公式能够描述\(s,s',R\)三者之间的数量关系,并且这个关系与\(\theta_1\)和\(\theta_2\)的值无关。
当研究对象为近轴光线时(即当\(\alpha\)非常小时),\(\alpha,\beta,\phi,\theta_1,\theta_2,\delta\)的值均非常小。
此时,\((4.1)\)可以表示为
\[ \begin{equation} n_1 \theta_1 = n_2 \theta_2 \end{equation} \tag{4.4} \]
\((4.3)\)可以表示为
\[ \begin{equation} \begin{aligned} \alpha &= \frac{h}{s} \\ \beta &= \frac{h}{s'} \\ \phi &= \frac{h}{R} \end{aligned} \end{equation} \tag{4.5} \]
将\((4.2)\)代入\((4.4)\),得
\[ \begin{equation} \begin{aligned} n_1 (\alpha + \phi) &= n_2 (\phi - \beta) \\ n_1 \alpha + n_1 \phi &= n_2 \phi - n_2 \beta \\ n_1 \alpha + n_2 \beta &= (n_2 - n_1) \phi \end{aligned} \end{equation} \tag{4.6} \]
将\((4.5)\)代入\((4.6)\),得
\[ \begin{equation} \begin{aligned} n_1 \frac{h}{s} + n_2 \frac{h}{s'} &= (n_2 - n_1) \frac{h}{R} \\ \end{aligned} \end{equation} \tag{4.7} \]
化简上式,我们将得到凸面折射时,\(s,s',R\)三者之间的数量关系
\[ \begin{equation} \frac{n_1}{s} + \frac{n_2}{s'} = \frac{n_2 - n_1}{R} \end{equation} \tag{4.8} \]
凹面折射

根据三角形内角与外角的关系,得
\[ \begin{equation} \begin{aligned} \theta_1 &= \phi - \alpha \\ \theta_2 &= \phi - \beta \end{aligned} \end{equation} \tag{4.9} \]
我们研究的对象仅限近轴光线。所以
折射定律可表示为
\[ \begin{equation} n_1 \theta_1 = n_2 \theta_2 \end{equation} \tag{4.10} \]
\(\tan\)函数可以表示为
\[ \begin{equation} \begin{aligned} \alpha &= \frac{h}{s} \\ \beta &= \frac{h}{-s'} \\ \phi &= \frac{h}{-R} \end{aligned} \end{equation} \tag{4.11} \]
将\((4.9)\)代入\((4.10)\),得
\[ \begin{equation} \begin{aligned} n_1 (\phi - \alpha) &= n_2 (\phi - \beta) \\ n_1 \alpha - n_2 \beta &= (n_1 - n_2) \phi \end{aligned} \end{equation} \tag{4.12} \]
将\((4.11)\)代入\((4.12)\),得
\[ \begin{equation} \begin{aligned} n_1 \frac{h}{s} - n_2 \frac{h}{-s'} &= (n_1 - n_2) \frac{h}{-R} \end{aligned} \end{equation} \tag{4.13} \]
化简上式,我们将得到凹面折射时,\(s,s',R\)三者之间的数量关系
\[ \begin{equation} \frac{n_1}{s} + \frac{n_2}{s'} = \frac{n_2 - n_1}{R} \end{equation} \tag{4.14 球面折射的物像公式} \]
注意\((4.8)\)和\((4.14)\)是相同的,不论是凸面折射还是凹面折射。
球面折射成像

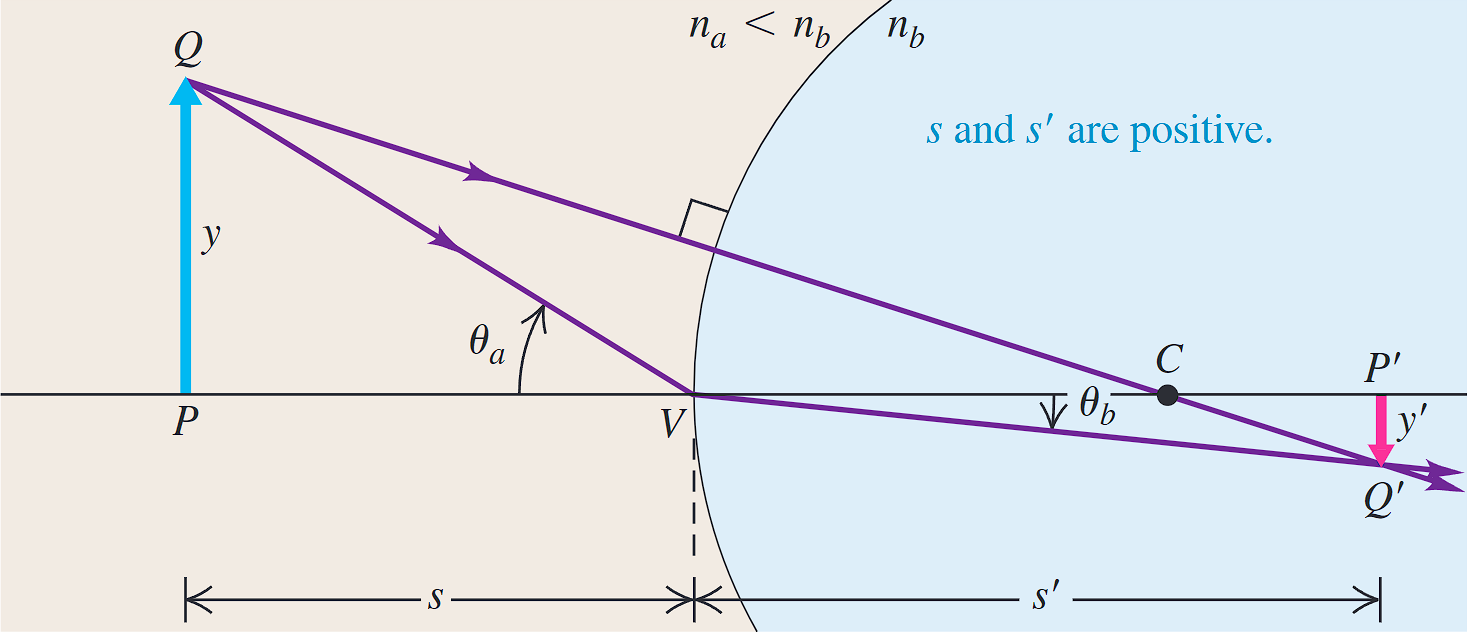
图1是我自己用PhyDemo绘制的,模拟不出球面折射的理想情况。所以附上图2(截图自教材University Physics with Modern Physics)来说明。
如图2所示,一个延展物体位于凸面透镜之前,在透镜内形成了一个倒立的实像。我们想要知道球面折射成像时的侧向放大率公式。
根据三角函数,有
\[ \tan{\theta_a} = \frac{y}{s}, \tan{\theta_b} = \frac{-y'}{s'} \]
根据折射定律,有
\[ n_a \sin{\theta_a} = n_b \sin{\theta_b} \]
当角度非常小时,有
\[ \tan{\theta_a} = \sin{\theta_a}, \tan{\theta_b} = \sin{\theta_b} \]
所以
\[ n_a \frac{y}{s} = -n_b \frac{y'}{s'} \]
于是
\[ \begin{equation} m = \frac{y'}{y} = -\frac{n_a s'}{n_b s} \end{equation} \tag{4.15 球面折射的侧向放大率公式} \]
公式\((4.15)\)也适用于凹面透镜。
凹面透镜成像就不分析了。更重要的是对薄透镜的分析。
薄透镜
透镜制造者公式
我们在此讨论的薄透镜是指,由符合球面折射的物像公式\((4.14)\)的两个间距为0的单折射球面组成的光学物件。薄透镜两侧透面的曲率分别为\(R_1,R_2\),透镜内部的折射率为\(n\),空气的折射率为\(1\)。
根据公式\((4.14)\),物对于第一个透面形成的像,有
\[ \frac{1}{s_1} + \frac{n}{s'_1} = \frac{n-1}{R_1} \]
第一个透面形成的像可以作为第二个透面的物,\(s_2 = -s'_1\)。这里取负号,是因为第一个像相对第二个面不处于入射光线一侧。继续套用公式\((4.14)\),有
\[ \frac{n}{s_2} + \frac{1}{s'_2} = \frac{1-n}{R_2} \]
于是
\[ \frac{1}{s_1} + \frac{n}{s'_1} + \frac{n}{s_2} + \frac{1}{s'_2} = \frac{n-1}{R_1} + \frac{1-n}{R_2} \\ \]
因为\(\frac{n}{s'_1} + \frac{n}{s_2} = 0\), 所以
\[ \begin{equation} \frac{1}{s_1} + \frac{1}{s'_2} = (n - 1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right) \end{equation} \tag{5.1 透镜制造者公式} \]
焦距
\[ f=(n - 1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right) \]
薄透镜的侧向放大率
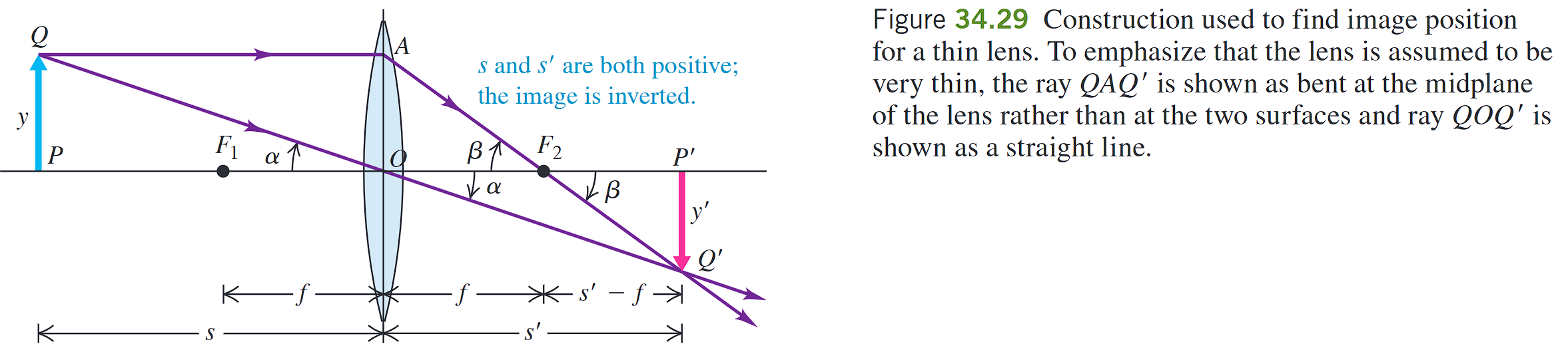
如图,
\[ \frac{y}{s} = \frac{-y'}{s'} \]
所以侧向放大率为
\[ m = \frac{y'}{y} = -\frac{s'}{s} \]
逐次成像法
对于更一般的情况,我们想知道物在经过一系列透面之后的成像。
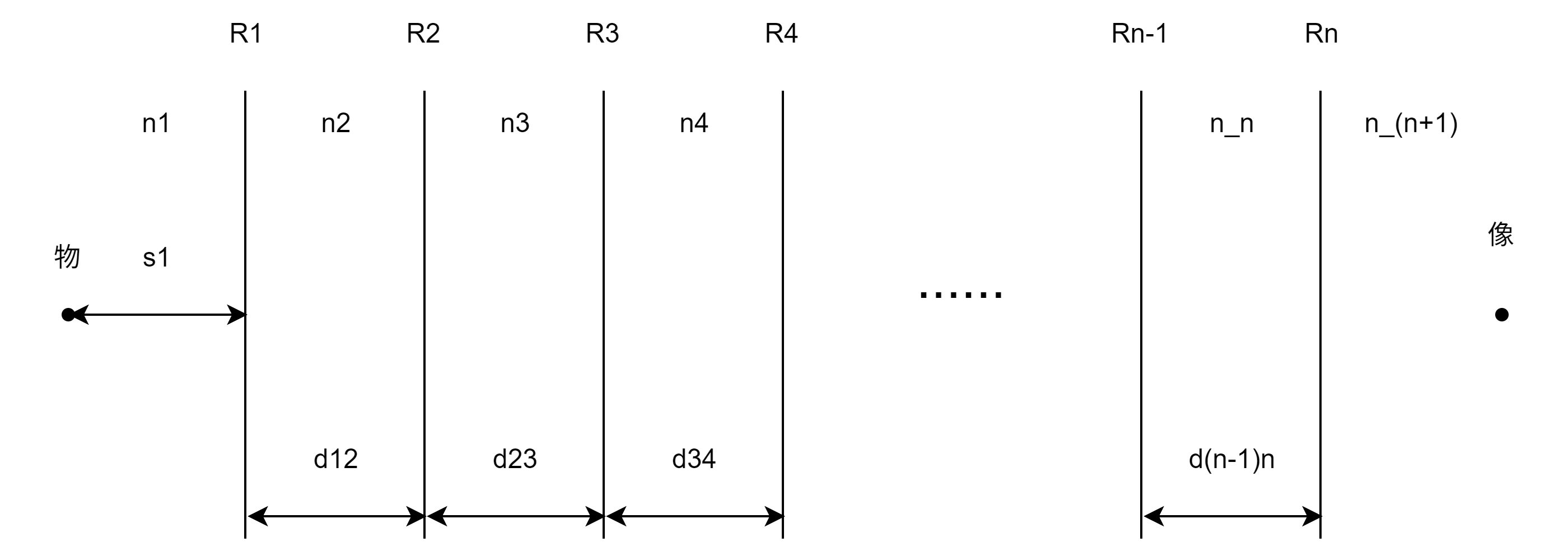
如图,在空间中有\(n\)个单折射透面。我们通过反复套用公式\((4.14)\),有
\[ \left\{ \begin{aligned} \frac{n_1}{s_1} + \frac{n_2}{d_{12} - s_2} = \frac{n_2 - n_1}{R_1} \\ \frac{n_2}{s_2} + \frac{n_3}{d_{23} - s_3} = \frac{n_3 - n_2}{R_2} \\ \frac{n_3}{s_3} + \frac{n_4}{d_{34} - s_4} = \frac{n_4 - n_3}{R_3} \\ \frac{n_4}{s_4} + \frac{n_5}{d_{45} - s_5} = \frac{n_5 - n_4}{R_4} \\ \cdots \\ \frac{n_n}{s_n} + \frac{n_{n+1}}{s'_n} = \frac{n_{n+1} - n_n}{R_n} \end{aligned} \right. \]
因为\(s_1,n_i,R_i,d_{ij}\)为已知量,所以我们能够得到最终像距\(s'_n\)。