一阶线性微分方程求解的两种方法
一阶线性微分方程求解的两种方法
定义
一阶线性微分方程(A first order linear differential equation)是能够被表示为以下形式的等式:
\[ \frac{d y}{d x} + p(x)y = f(x) \]
当\(f(x)=0\)时,等式被称作一阶齐次线性微分方程(A first order homogeneous linear differential equation):
\[ \frac{d y}{d x} + p(x)y = 0 \]
求解:一阶齐次线性微分方程
在求解一阶线性微分方程之前,我们需要先了解一阶齐次线性微分方程的求解方法。
一阶齐次线性微分方程\(\frac{dy}{dx} + p(x)y = 0\)的通解(the general solution)为:
\[ y = C_1 e^{- P(x)} \]
为方便起见,令\(\int p(x) dx = P(x)\)。(在后续的内容中,我们将遵从这个约定。)
证明:
\[ \begin{aligned} \frac{dy}{dx} + p(x)y &= y \\ \frac{dy}{dx} &= -p(x)y \\ \frac{1}{y} dy &= -p(x) dx \\ \int \frac{1}{y} dy &= - \int p(x) dx \\ \ln{|y|} &= - P(x) + C \\ |y| &= e^{- P(x) + C} \\ y &= \pm e^{C} e^{- P(x)} \\ y &= C_1 e^{- P(x)} \hspace{1cm}\blacksquare \end{aligned} \]
其中,\(C_1 = \pm e^{C}\)。
求解:一阶线性微分方程
方法1:参数变分(variation of parameters)
采用这种方法求解,我们将认为一阶线性微分方程\(\frac{d y}{d x} + p(x)y = f(x)\)的解的形式为:\(y=v(x)h(x)\)。其中\(h(x)\)是此方程对应的齐次方程的特解:\(h(x)=e^{-P(x)}\);\(v(x)\)则是“variation of parameters.”(我的理解是,\(v(x)\)可以被视作一种解题技巧。)
如果
\[ y=v(x)h(x) \]
那么
\[ \begin{aligned} y' + p(x)y &= (v(x)h(x))' + p(x)v(x)h(x) \\ &= v'(x)h(x) + v(x)h'(x) + p(x)v(x)h(x) \\ &= v'(x)h(x) + v(x)(h'(x) + p(x)h(x)) \\ &= v'(x)h(x) \\ &= f(x) \end{aligned} \]
注意:因为\(h(x)\)为齐次方程的解,所以\(h'(x) + p(x)h(x)=0\)。
因此,我们得到:
\[ v'(x) = \frac{f(x)}{h(x)} \text{, therefore } v(x) = \int \frac{f(x)}{h(x)} dx + C \text{.} \]
最后,我们得到:
\[ \begin{aligned} y &= v(x)h(x) \\ &= \left( \int \frac{f(x)}{h(x)} dx + C \right) h(x) \end{aligned} \]
注意:在开头我们定义了\(h(x)=e^{-P(x)}\),但我们也可以定义\(h(x)= C_1 e^{-P(x)}\),因为\(y=v(x)h(x)=(\int \frac{f(x)}{h(x)} dx) h(x) = (\frac{1}{C_1} \int \frac{f(x)}{e^{-P(x)}} dx) C_1 e^{-P(x)}=(\int \frac{f(x)}{e^{-P(x)}} dx) e^{-P(x)}\),在这里,\(C_1\)项会被约去。前一种定义是教科书上常用的定义。
方法2:积分因子(Integrating Factor)
采用这种方法求解,我们先将一阶线性微分方程列出:
\[ \frac{d y}{d x} + p(x)y = f(x) \]
在方程的左右两侧同时乘上积分因子\(μ(x)\):
\[ μ(x)\frac{d y}{d x} + μ(x)p(x)y = μ(x)f(x) \]
接着,我们希望\(μ(x)\)满足:
\[ (μ(x)y)' = μ(x)\frac{d y}{d x} + μ(x)p(x)y = μ(x)f(x) \]
为什么要满足这个条件呢,我将之视作又一个解题技巧,利用了乘积法则(the
product rule)。
如果:
\[ (μ(x)y)' = μ(x)f(x) \]
那么:
\[ \begin{aligned} \frac{dμ(x)y}{dx} &= μ(x)f(x) \\ \int dμ(x)y &= \int μ(x)f(x) dx \\ μ(x)y &= \int μ(x)f(x) dx + C \\ y &= \frac{\int μ(x)f(x) dx + C}{μ(x)} \end{aligned} \]
由此,我们便得到通解 \[ y = \frac{\int μ(x)f(x) dx + C}{μ(x)} \]
下一步我们需要找出\(μ(x)\):
如果:
\[ (μ(x)y)' = μ(x)\frac{d y}{d x} + μ(x)p(x)y \]
那么:
\[ \begin{aligned} μ(x)\frac{d y}{d x} + μ'(x)y &= μ(x)\frac{d y}{d x} + μ(x)p(x)y\\ μ'(x)y &= μ(x)p(x)y \\ μ'(x) &= μ(x)p(x) \\ \frac{dμ(x)}{dx} &= μ(x)p(x) \\ \frac{1}{μ(x)} dμ(x) &= p(x) dx \\ \int \frac{1}{μ(x)} dμ(x) &= \int p(x) dx \\ \ln |μ(x)| &= P(x) + C \\ μ(x) &= \pm e^C e^{P(x)} \\ μ(x) &= C_1 e^{P(x)} \end{aligned} \]
因为\(μ(x) = C_1 e^{P(x)}\),所以一阶线性微分方程\(\frac{d y}{d x} + p(x)y = f(x)\)的通解为:
\[ y = \frac{\int e^{P(x)} f(x) dx}{e^{P(x)}} + C e^{-P(x)} \]
或者(令\(h(x)=e^{-P(t)}\))
\[ y = \left( \int \frac{f(x)}{h(x)} dx + C \right) h(x) \]
注意:这和我们通过第一种方法得到的通解是一样的。
小结
一阶齐次线性微分方程
\[ \frac{d y}{d x} + p(x)y = 0 \]
的通解为
\[ y(x) = C e^{-P(x)} \text{, where } P(x) = \int p(x) dx \]
;
一阶线性微分方程
\[ \frac{d y}{d x} + p(x)y = f(x) \]
的通解为
\[ y = \left( \int \frac{f(x)}{h(x)} dx + C \right) h(x) \text{, where } h(x) = e^{-P(x)} \]
。
参考资料
The
Ordinary Differential Equations Project
Calculus
Early Transcendentals: Integral & Multi-Variable Calculus for Social
Sciences
Elementary
Differential Equations with Boundary Value Problems
应用
RC直流电路分析–充放电公式
充电过程
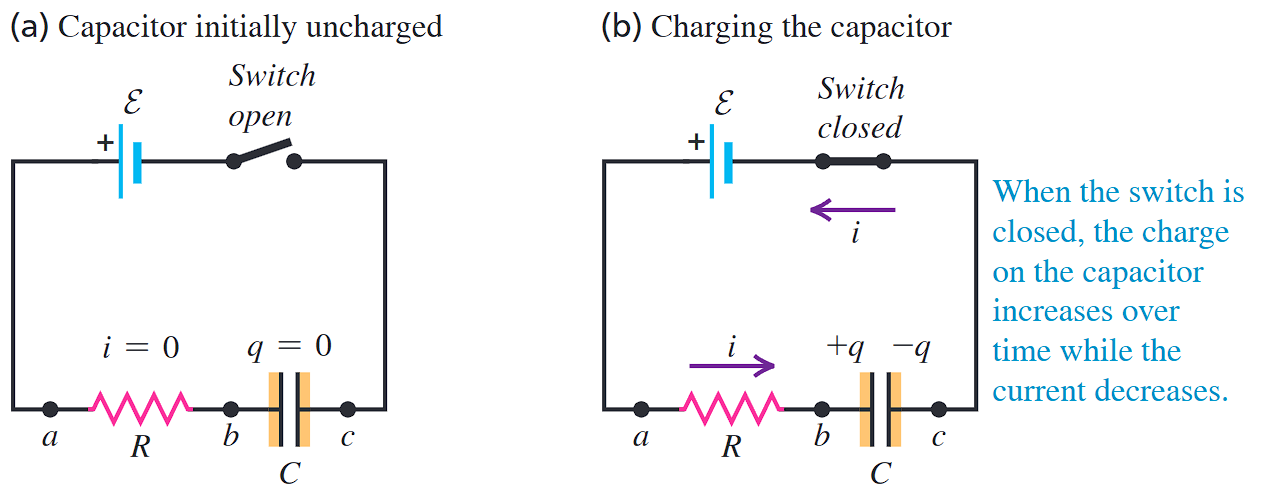
如图所示,这是一个RC直流电路(电动势\(\mathcal{E}\),电阻\(R\),电容\(C\))。
电路最初处于状态(a),我们可以据此得到初值条件
\[ q(t=0) = 0 \tag{1} \]
闭合电路后,我们得到状态(b)。根据基尔霍夫定律我们可知\(v_\text{ab} + v_{\text{bc}} = v_{\text{ac}}\),即
\[ i R + \frac{q}{C} = \mathcal{E} \text{ where } i = \frac{\mathrm{d} q}{\mathrm{d} t} \tag{2} \]
将(2)写成一阶线性微分方程的标准形式
\[ q' + \frac{1}{R C} q = \frac{\mathcal{E}}{R} \tag{3} \]
于是有 \[ \begin{equation} \begin{aligned} p(t) &= \frac{1}{R C} \\ f(t) &= \frac{\mathcal{E}}{R} \\ h(t) &= e^{-\int p(t) \mathrm{d} t } = e^{-\frac{t}{R C}} \\ q(t) &= \left(\int \frac{f(t)}{h(t)} \mathrm{d} t + C_1 \right) h(t) \\ &= \left( \frac{\mathcal{E}}{R} \int e^{\frac{t}{R C}} \mathrm{d} t + C_1 \right) e^{-\frac{t}{R C}} \\ &= (C \mathcal{E} e^{\frac{t}{R C}} + C_1) e^{-\frac{t}{R C}} \\ &= C \mathcal{E} + C_1 e^{-\frac{t}{R C}} \end{aligned} \tag{4} \end{equation} \]
将初值条件(1)代入(4)可得\(C_1\)
\[ \begin{equation} \begin{aligned} q(0) &= C \mathcal{E} + C_1 e^{-\frac{0}{R C}} \\ &= C \mathcal{E} + C_1 \\ &= 0 \\ \implies C_1 &= - C \mathcal{E} \end{aligned} \tag{5} \end{equation} \]
将(5)代入(4)得
\[ \begin{equation} \begin{aligned} q(t) &= C \mathcal{E} - C \mathcal{E} e^{-\frac{t}{R C}} \\ &= C \mathcal{E} (1 - e^{-\frac{t}{R C}}) \end{aligned} \tag{6} \end{equation} \]
又得
\[ \begin{equation} \begin{aligned} i(t) &= \frac{\mathrm{d} q}{\mathrm{d} t} \\ &= C \mathcal{E} e^{-\frac{t}{R C}} \end{aligned} \tag{7} \end{equation} \]
至此,我们得到了RC直流电路充电过程的\(q(t),i(t)\)的函数表达式\((6),(7)\)。
放电过程
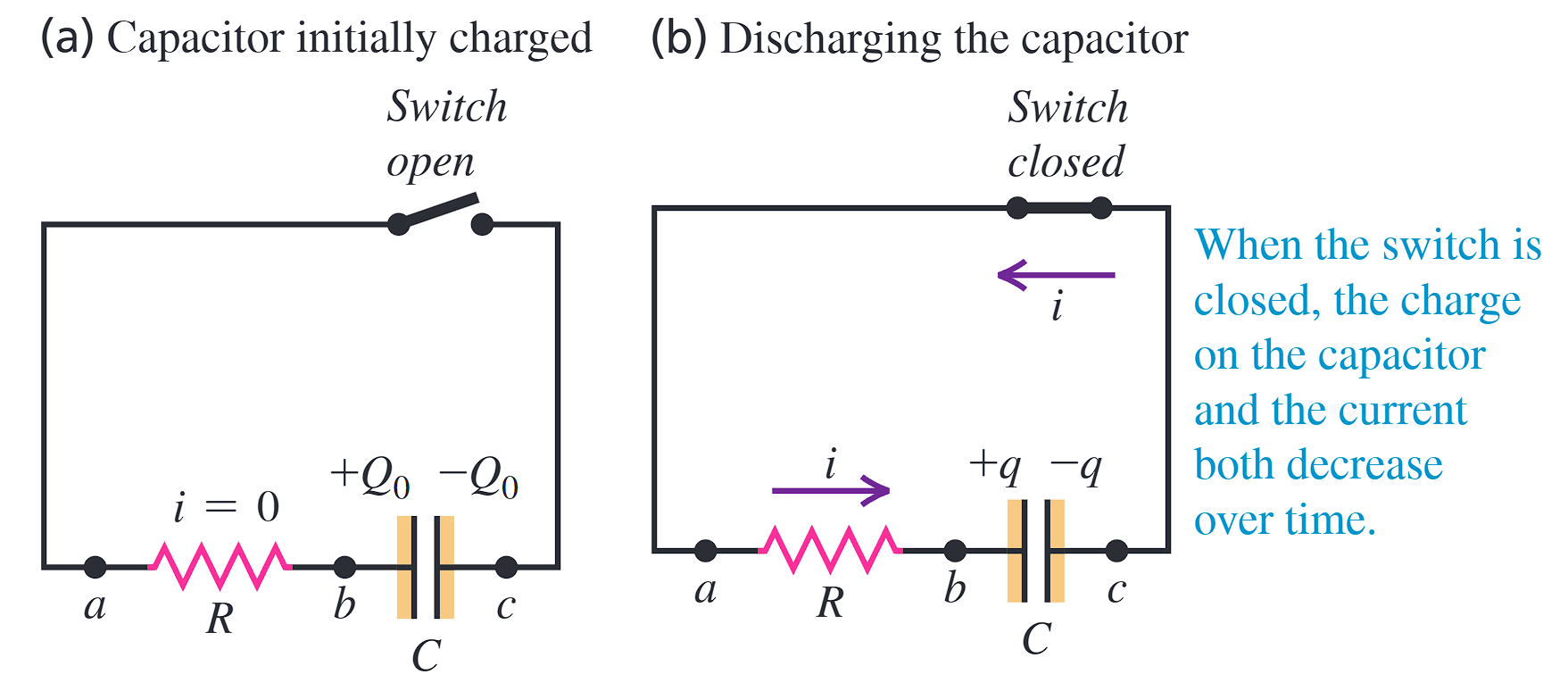
如图所示,这是一个RC直流电路(电阻\(R\),电容\(C\))。
电路最初处于状态(a),我们可以据此得到初值条件
\[ q(t = 0) = Q_0 \tag{1} \]
闭合电路后,我们得到状态(b)。根据基尔霍夫定律我们可知\(v_\text{ab} + v_{\text{bc}} = 0\),即
\[ i R + \frac{q}{C} = 0 \tag{2} \]
将(2)写成一阶线性微分方程的标准形式
\[ q' + \frac{1}{R C} q = 0 \tag{3} \]
这是一阶齐次线性微分方程,故其通解为
\[ q(t) = C_1 e^{-\frac{t}{R C}} \tag{4} \]
将初值条件(1)代入(4)得
\[ \begin{equation} \begin{aligned} q(0) &= C_1 \\ &= Q_0 \end{aligned} \tag{5} \end{equation} \]
将(5)代入(4)得
\[ q(t) = Q_0 e^{-\frac{t}{R C}} \tag{6} \]
又得
\[ \begin{equation} \begin{aligned} i(t) &= \frac{\mathrm{d} q}{\mathrm{d} t} \\ &= - \frac{Q_0}{R C} e^{-\frac{t}{R C}} \end{aligned} \tag{7} \end{equation} \]
至此,我们得到了RC直流电路放电过程的\(q(t),i(t)\)的函数表达式\((6),(7)\)。