三角函数常用公式

这篇笔记用于记录一些我在学习过程中经常使用到的三角函数公式。我会给我认为关键的几个公式列出证明。

定义 \(\sin,\cos,和\tan.\)

\[ \cos(\theta)=\frac{x}{r} \]

\[ \sin(\theta)=\frac{y}{r} \]

\[ \tan(\theta)=\frac{\sin(\theta)}{\cos(\theta)}=\frac{y}{x} \]

其中，\(r\)代表圆半径。

另外，我在网上发现的一个优秀的三角函数可视化作品：The Etymology of Trig Functions

基本定理

\[ \cos(-\theta)=\cos(\theta) \]

\[ \sin(-\theta)=-\sin(\theta) \]

\[ \frac{d \cos(\theta)}{d t}=-\sin(\theta) \]

\[ \frac{d \sin(\theta)}{d t}=\cos(\theta) \]

\[ \cos^2(\theta)+\sin^2(\theta)=1 \]

\[ \sin(\alpha)=\cos(\beta)\text{, where }\alpha+\beta=\frac{\pi}{2}. \]

这一部分内容直接记忆，难度不大。

和差角公式

\[ \cos(\alpha\mp\beta)=\cos(\alpha)\cos(\beta)\pm\sin(\alpha)\sin(\beta) \]

\[ \sin(\alpha\pm\beta)=\sin(\alpha)\cos(\beta)\pm\cos(\alpha)\sin(\beta) \]

倍角、半角公式

倍角

\[ \begin{aligned} \cos(2\theta) &= \cos^2(\theta) - \sin^2(\theta) \\ &= 2\cos^2(\theta) - 1 \\ &= 1 - 2\sin^2(\theta) \end{aligned} \]

\[ \begin{aligned} \sin(2\theta) &= 2 \sin(\theta) \cos(\theta) \\ \end{aligned} \]

通过和角公式推导得出。

半角

\[ \cos(\frac{\theta}{2})=\pm\sqrt{\frac{1 + \cos{\theta}}{2}} \]

\[ \sin(\frac{\theta}{2})=\pm\sqrt{\frac{1 - \cos{\theta}}{2}} \]

或者

\[ \cos^2(\frac{\theta}{2})=\frac{1 + \cos{\theta}}{2} \]

\[ \sin^2(\frac{\theta}{2})=\frac{1 - \cos{\theta}}{2} \]

通过倍角公式推导得出。

其中，后两个涉及平方形式的公式，在计算交流电路平均功率\(P_{av}\)时，使用过。(\(\int\sin^2 x\ dx=\int \frac{1-\cos(2x)}{2} \ dx\))

积化和差与和差化积公式

积化和差公式

\[ \sin(\alpha)\sin(\beta)=\frac{1}{2}[\cos(\alpha-\beta)-\cos(\alpha+\beta)] \]

\[ \cos(\alpha)\cos(\beta)=\frac{1}{2}[\cos(\alpha-\beta)+\cos(\alpha+\beta)] \]

\[ \sin(\alpha)\cos(\beta)=\frac{1}{2}[\sin(\alpha+\beta)+\sin(\alpha-\beta)] \]

通过和差角公式推导得出。

和差化积公式

\[ \sin(\alpha)+\sin(\beta)=2\sin(\frac{\alpha+\beta}{2})\cos(\frac{\alpha-\beta}{2}) \]

\[ \cos(\alpha)+\cos(\beta)=2\cos(\frac{\alpha+\beta}{2})\cos(\frac{\alpha-\beta}{2}) \]

推导上述公式的过程中有一个小技巧，需要构造这样的等式：
\(\alpha=\frac{(\alpha+\beta)+(\alpha-\beta)}{2}\), 和
\(\beta=\frac{(\alpha+\beta)-(\alpha-\beta)}{2}\).

关于\(\sin(\alpha)+\cos(\beta)\)，我简单地搜索了一下，没有直接的公式。

欧拉公式

\[ e^{i \theta}=\cos{\theta}+i\sin{\theta} \]

在学习微分方程的时候遇见过。

证明

\(\cos(\alpha-\beta)=\cos(\alpha)\cos(\beta)+\sin(\alpha)\sin(\beta)\)

证明这个公式之后，剩余的公式都可以很容易地推导出来。

Proof.

Step 1. 作图：

cos(alpha_minus_beta)

Step 2. 列等式：

如图所示，线段\(PQ=AB\)(全等三角形)。
因为\(PQ=\sqrt{(\cos(\alpha)-\cos(\beta))^2+(\sin(\alpha)-\sin(\beta))^2},AB=\sqrt{(\cos(\alpha-\beta)-1)^2+\sin^2(\alpha-\beta)}\).
所以

\[ \begin{aligned} \sqrt{(\cos(\alpha)-\cos(\beta))^2+(\sin(\alpha)-\sin(\beta))^2} &= \sqrt{(\cos(\alpha-\beta)-1)^2+\sin^2(\alpha-\beta)} \\ (\cos(\alpha)-\cos(\beta))^2+(\sin(\alpha)-\sin(\beta))^2 &= (\cos(\alpha-\beta)-1)^2+\sin^2(\alpha-\beta) \\ \cos^2(\alpha)-2\cos(\alpha)\cos(\beta)+\cos^2(\beta)+\sin^2(\alpha)-2\sin(\alpha)\sin(\beta)+\sin^2(\beta) &= \cos^2(\alpha-\beta)-2\cos(\alpha-\beta)+1+\sin^2(\alpha-\beta) \\ 2 - 2[\cos(\alpha)\cos(\beta) + \sin(\alpha)\sin(\beta)] &= 2 - 2\cos(\alpha-\beta) \\ \cos(\alpha)\cos(\beta) + \sin(\alpha)\sin(\beta) &= \cos(\alpha-\beta) \hspace{5cm}\blacksquare\\ \end{aligned} \]

应用

纯电阻交流电路的平均功率

purely resistive AC circuit

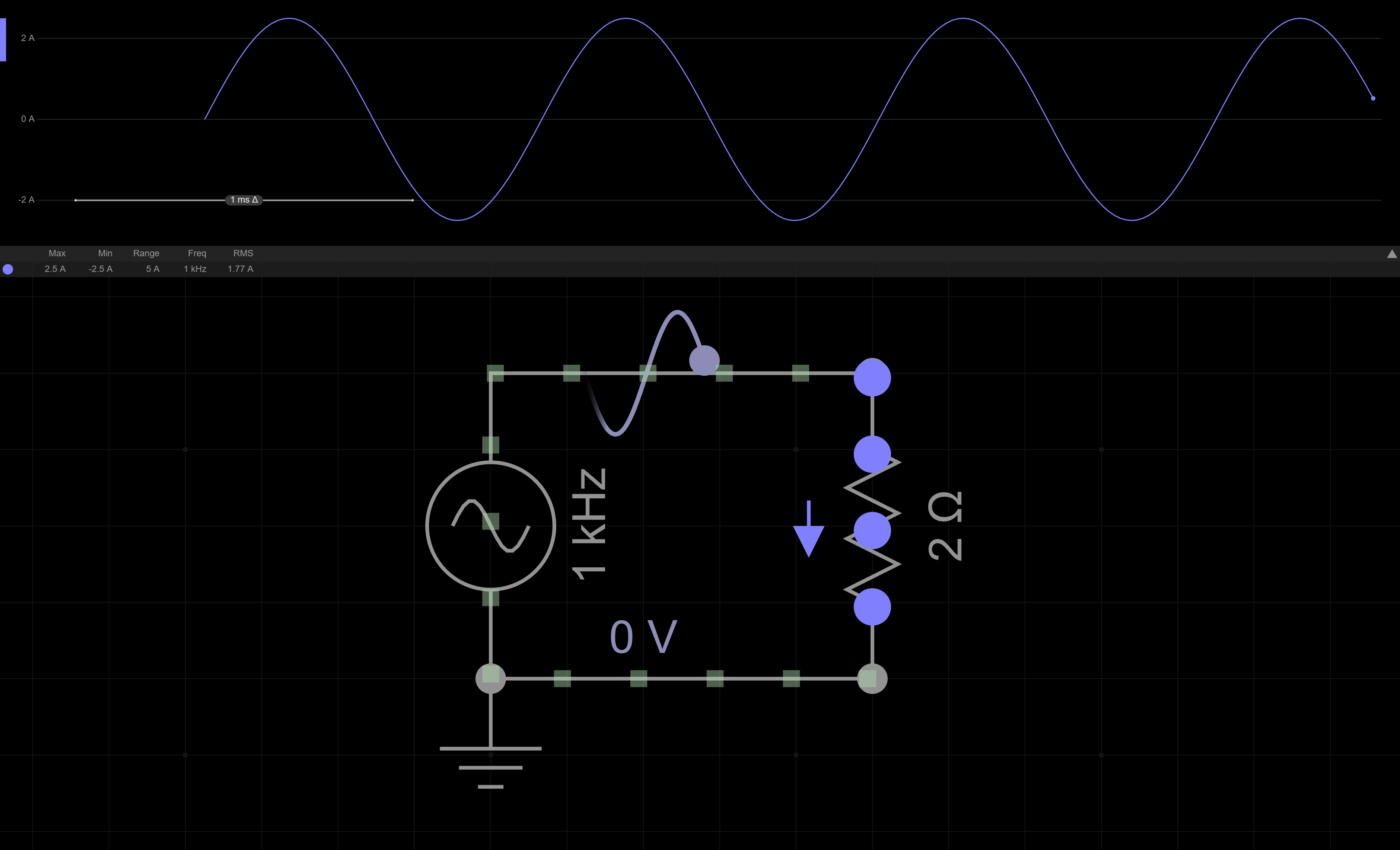
如图(用EveryCircuit制作)，这是一个纯电阻交流电路，其中交流电压:\(v = V_{\text{max}} \sin(2\pi f t),(V_{\text{max}}=5 \text{V}, f = 1000 \text{Hz}\))，电阻:\(R=2 \Omega\)。根据欧姆定律\(I = \frac{V}{R}\)，我们可以得到电路电流的表达式： \[ i=\frac{v}{R}=\frac{V_{\text{max}}}{R} \sin(2\pi f t) \] 根据电功率公式\(P=I^2 R\)可知： \[ p=i^2R=\frac{V_{\text{max}}^2}{R} \sin^2(2\pi f t) = I_{\text{max}}^2 R \sin^2(2\pi f t) \] 于是，我们得到了瞬时功率\(p\)的表达式。接着，我们想要知道电路的平均功率可以利用微积分计算\(p\)在一个周期\(T=\frac{1}{f}\)中所做的总功\(W_T\)，再除以周期\(T\),便能得到平均功率\(P_{\text{av}}=\frac{W_T}{T}\)。 \[ \begin{align} P_{\text{av}} &= \frac{W_T}{T} \\ &= \frac{\int^{1/f}_0 i^2R\ \mathrm{d} t}{1/f} \\ &= I_{\text{max}}^2 R f \int^{1/f}_0 \sin^2(2\pi f t)\ \mathrm{d} t \\ &= I_{\text{max}}^2 R f \int^{1/f}_0 \frac{1 - \cos{4 \pi f t}}{2}\ \mathrm{d} t \\ &= I_{\text{max}}^2 R f \left( \frac{t}{2} - \frac{\sin{4 \pi f t}}{8 \pi f} \right) \bigg|^{1/f}_{0} \\ &= I_{\text{max}}^2 R f \frac{1}{2f} \\ &= \frac{1}{2}I_{\text{max}}^2 R = \frac{V_{\text{max}}^2}{2R} = \frac{1}{2} V_{\text{max}} I_{\text{max}} \end{align} \]

注意，在上述公式推导中，(3)到(4)的化简利用了半角公式。

至此，我们得到了纯电阻交流电路中\(P_\text{av},I_{\text{max}},V_{\text{max}},R\)之间的数值关系。
我推导这个公式的主要目的是为了介绍半角公式的使用。在这里，半角公式作为化简积分的一种技巧而被使用。

简谐运动(SHM)公式推导

简谐运动的一般形式由胡克定律和牛顿第二定律结合得到：

\[ m\frac{\mathrm{d}^2 x}{\mathrm{d} t^2} + k x =0 \tag{1} \]

将其转化为线性方程组(linear homogeneous constant coefficient systems of ODEs)：

\[ \begin{equation} \left\{ \begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t} &= v \\ \frac{\mathrm{d}v}{\mathrm{d}t} &= -\frac{k}{m}x \end{aligned} \right. \tag{2} \end{equation} \]

为了求此系统的解，我们引入以下定理：

如何得到这个定理请参考链接：
3.4: Eigenvalue Method
3.4 Complex Eigenvalues

Theorem 1

对于线性方程组\(\mathbf{x}'=A\mathbf{x}\)，假设矩阵\(A\)是一个大小为\(2\times 2\)的常数矩阵。如果\(A\)有一个复特征值\(a + b i\)和相应的复特征向量\(\mathbf{v}\)，那么这个线性方程组的通解为：

\[ \mathbf{x}=c_1 \Re\left[e^{(a+ib)t}\mathbf{v}\right] + c_2 \Im\left[e^{(a+ib)t}\mathbf{v}\right] \]

将线性方程组\((2)\)写作\(\mathbf{x}'=A\mathbf{x}\)的形式：

\[ \begin{pmatrix} x' \\ v' \end{pmatrix} = \begin{pmatrix} 0 & 1 \\ -\frac{k}{m} & 0 \end{pmatrix} \begin{pmatrix} x \\ v\end{pmatrix} \tag{3} \]

求出矩阵\(A\)的特征值为\(\lambda = i\sqrt{\frac{k}{m}}\)，相应的特征向量为\(\mathbf{v} = \begin{pmatrix} 1 \\ i\sqrt{\frac{k}{m}}\end{pmatrix}\)。

根据Theorem 1，我们得到通解：

\[ \begin{pmatrix} x \\ v\end{pmatrix} = c_1 \Re\left[e^{i\sqrt{\frac{k}{m}}t} \begin{pmatrix} 1 \\ i\sqrt{\frac{k}{m}}\end{pmatrix}\right] + c_2 \Im\left[e^{i\sqrt{\frac{k}{m}}t}\begin{pmatrix} 1 \\ i\sqrt{\frac{k}{m}}\end{pmatrix}\right] \tag{4} \]

根据欧拉公式可得：

\[ e^{i\sqrt{\frac{k}{m}}t} = \cos{\left( \sqrt{\frac{k}{m}}t \right)} + i \sin{\left( \sqrt{\frac{k}{m}}t \right)} \tag{5} \]

将\((5)\)带入(4)得：

\[ \begin{equation} \begin{aligned} \begin{pmatrix} x \\ v\end{pmatrix} &= c_1 \Re\left\{\left[ \cos{\left( \sqrt{\frac{k}{m}}t \right)} + i \sin{\left( \sqrt{\frac{k}{m}}t \right)} \right] \begin{pmatrix} 1 \\ i\sqrt{\frac{k}{m}}\end{pmatrix}\right\} + c_2 \Im\left\{\left[ \cos{\left( \sqrt{\frac{k}{m}}t \right)} + i \sin{\left( \sqrt{\frac{k}{m}}t \right)} \right]\begin{pmatrix} 1 \\ i\sqrt{\frac{k}{m}}\end{pmatrix}\right\} \\ &= c_1 \Re\left[ \begin{pmatrix} \cos{\left( \sqrt{\frac{k}{m}}t \right)} + i \sin{\left( \sqrt{\frac{k}{m}}t \right)} \\ i\sqrt{\frac{k}{m}}\cos{\left( \sqrt{\frac{k}{m}}t \right)} - \sqrt{\frac{k}{m}} \sin{\left( \sqrt{\frac{k}{m}}t \right)} \end{pmatrix} \right] + c_2 \Im\left[ \begin{pmatrix} \cos{\left( \sqrt{\frac{k}{m}}t \right)} + i \sin{\left( \sqrt{\frac{k}{m}}t \right)} \\ i\sqrt{\frac{k}{m}}\cos{\left( \sqrt{\frac{k}{m}}t \right)} - \sqrt{\frac{k}{m}} \sin{\left( \sqrt{\frac{k}{m}}t \right)} \end{pmatrix} \right] \\ &=c_1 \begin{pmatrix} \cos{\left( \sqrt{\frac{k}{m}}t \right)} \\ -\sqrt{\frac{k}{m}} \sin{\left( \sqrt{\frac{k}{m}}t \right)} \end{pmatrix} + c_2 \begin{pmatrix} \sin{\left( \sqrt{\frac{k}{m}}t \right)} \\ \sqrt{\frac{k}{m}}\cos{\left( \sqrt{\frac{k}{m}}t \right)} \end{pmatrix} \\ &= \begin{pmatrix} \cos{\left( \sqrt{\frac{k}{m}}t \right)} & \sin{\left( \sqrt{\frac{k}{m}}t \right)} \\ -\sqrt{\frac{k}{m}} \sin{\left( \sqrt{\frac{k}{m}}t \right)} & \sqrt{\frac{k}{m}}\cos{\left( \sqrt{\frac{k}{m}}t \right)} \end{pmatrix} \begin{pmatrix} c_1 \\ c_2 \end{pmatrix} \end{aligned} \tag{6} \end{equation} \]

为了求出常数\(c_1,c_2\)的值，我们需要处置条件。假设\(x(t=0)=X_{\text{max}},v(t=0)=0\)。(即此时物体位于最大位移处)
将初值条件带入\((6)\)解得：

\[ \begin{pmatrix} c_1 \\ c_2 \end{pmatrix} = \begin{pmatrix} X_{\text{max}} \\ 0 \end{pmatrix} \]

所以

\[ \begin{aligned} x(t) &= X_{\text{max}} \cos{\left( \sqrt{\frac{k}{m}}t \right)} \\ v(t) &= -\sqrt{\frac{k}{m}} X_{\text{max}} \sin{\left( \sqrt{\frac{k}{m}}t \right)} \end{aligned} \]

至此我们得到了简谐运动的运动方程\(x(t),v(t)\)。
在求解过程中，我们使用到了欧拉公式\(e^{i \theta}=\cos{\theta}+i\sin{\theta}\)。